Week of March 27,2017

Algebra 1

Factoring Quadratics

A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can't be 0.)

To "Factor" (or "Factorise" in the UK) a Quadratic is to:

find what to multiply to get the Quadratic

It is called "Factoring" because we find the factors (a factor is something we multiply by)

Example

The factors of x² + 3x − 4 are:

(x+4) and (x−1)

Why? Well, let us multiply them to see:

(x+4)(x−1)	= x(x−1) + 4(x−1)
	= x2 − x + 4x − 4
	= x2 + 3x − 4

Multiplying (x+4)(x−1) together is called Expanding.

In fact, Expanding and Factoring are opposites:

Expanding is easy, but Factoring can often be tricky

It is like trying to find out what ingredients went into a cake to make it so delicious. It can be hard to figure out!

So let us try an example where we don't know the factors yet:

Common Factor

First check if there any common factors.

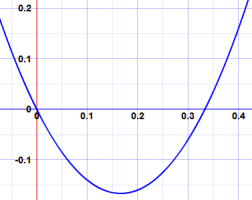
Example: what are the factors of 6x² − 2x = 0 ?

6 and 2 have a common factor of 2:

2(3x² − x) = 0

And x² and x have a common factor of x:

2x(3x − 1) = 0

And we have done it! The factors are 2x and 3x − 1,

We can now also find the roots (where it equals zero):

• 2x is 0 when x = 0
• 3x − 1 is zero when x = 1/3

And this is the graph (see how it is zero at x=0 and x=1/3):

But it is not always that easy ...

Guess and Check

Maybe we can guess an answer?

Example: what are the factors of 2x² + 7x + 3 ?

No common factors.

Let us try to guess an answer, and then check if we are right ... we might get lucky!

We could guess (2x+3)(x+1):

(2x+3)(x+1) = 2x² + 2x + 3x + 3
= 2x² + 5x + 3 (WRONG)

How about (2x+7)(x−1):

(2x+7)(x−1) = 2x² − 2x + 7x − 7
= 2x² + 5x − 7 (WRONG AGAIN)

OK, how about (2x+9)(x−1):

(2x+9)(x−1) = 2x² − 2x + 9x − 9
= 2x² + 7x − 9 (WRONG AGAIN)

Oh No! We could be guessing for a long time before we get lucky.

That is not a very good method. So let us try something else.

A Method For Simple Cases

Luckily there is a method that works in simple cases.

With the quadratic equation in this form:

Step 1: Find two numbers that multiply to give ac (in other words a times c), and add to give b.

Example: 2x² + 7x + 3

ac is 2×3 = 6 and b is 7

So we want two numbers that multiply together to make 6, and add up to 7

In fact 6 and 1 do that (6×1=6, and 6+1=7)

How do we find 6 and 1?

It helps to list the factors of ac=6, and then try adding some to get b=7.

Factors of 6 include 1, 2, 3 and 6.

Aha! 1 and 6 add to 7, and 6×1=6.

Step 2: Rewrite the middle with those numbers:

Rewrite 7x with 6x and 1x:

2x² + 6x + x + 3

Step 3: Factor the first two and last two terms separately:

The first two terms 2x² + 6x factor into 2x(x+3)

The last two terms x+3 don't actually change in this case

So we get:

2x(x+3) + (x+3)

Step 4: If we've done this correctly, our two new terms should have a clearly visible common factor.

In this case we can see that (x+3) is common to both terms, so we can go:

Start with		2x(x+3) + (x+3)
Which is:		2x(x+3) + 1(x+3)
And so:		(2x+1)(x+3)

Check: (2x+1)(x+3) = 2x² + 6x + x + 3 = 2x² + 7x + 3 (Yes)

Algebra 2

Assessments: Midterm on Wednesday

Monday
Today, we look at multiply and divide rational expressions
Help:http://www.purplemath.com/modules/rtnlmult.htm
HW; None

Tuesday
Combo day, ( simplify, multiply and divide) and rational equations
Help:https://www.khanacademy.org/math/algebra2/rational-expressions-equations-and-functions/multiplying-and-dividing-rational-expressions/e/multiplying_and_dividing_rational_expressions_3
HW: review for midterm

Wednesday
Midterm day and classwork time on rational equations
Help:http://www.purplemath.com/modules/solvrtnl.htm
HW: None

Thursday
A quick quiz today on the rational expressions and notes on word problems for rational equations
Help: https://www.khanacademy.org/math/algebra-home/alg-rational-expr-eq-func/alg-solving-rational-equations/v/rational-equations
HW: None

Friday
Make up for the 2nd 6 weeks, find what you need to make up and do it. If all work is done, challenge puzzles will be provided.
HW; none ( enjoy the break!)

Enjoy Spring Break! 6.5 weeks to go!

Week of March 20,2017

ALGEBRA 1

Choosing a Factoring Method

Step 1 Check for a greatest common factor. 
Step 2 Check for a pattern that fits the difference of two squares or a perfect-square trinomial. 
Step 3 To factor x 2 + bx + c, look for two numbers whose sum is b and whose product is c. To factor ax 2 + bx + c, check factors of a and factors of c in the binomial factors. The sum of the products of the outer and inner terms should be b.
 Step 4 Check for common factors.

Use the following table to help you choose a factoring method.

First factor out a GCF if possible.

Then, Explain how to choose a factoring method for x2 − x − 30. Then state the method. • There is no GCF. • x2 − x − 30 is a trinomial.

 • The terms a and b are not perfect squares, therefore this is not a perfect square trinomial. • a = 1 Method: Factor by checking factors of c that sum to b. Explain how to choose a factoring method for 2x2 − 50. Then state the method.

 • Factor out the GCF: 2(x2 − 25) • x2 − 25 is a binomial. • a and b are perfect squares. This is a difference of squares.

 If binomial, check for difference of squares. yes no Use (a + b)(a − b). If no GCF, it cannot be factored. If trinomial, check for perfect square trinomial. yes no Factor using (a + b) 2 or (a − b) 2 . If a = 1, check factors of c that sum to b. If a ≠ 1, check inner plus outer factors of a and c that sum to b. If 4 or more terms, Try to factor by grouping.

ALGEBRA 2

Assessments: Unit project on Thursday

Monday
Today, we look at characteristics of polynomials ( intercepts, roots, extrema)
Help:http://www.coolmath.com/precalculus-review-calculus-intro/precalculus-algebra/12-relative-extrema-minimums-maximums-01
HW; None

Tuesday
It is a day of review for the characteristics of Polynomials and finding roots of polynomials, a full day all about polynomials.
Help:https://www.sophia.org/tutorials/characteristics-of-polynomials
HW; None

Wednesday
It is a day of review of all things polynomials and a look at end behavior, with discovery mixed in.
Help:https://www.khanacademy.org/math/algebra2/polynomial-functions/polynomial-end-behavior/v/polynomial-end-behavior
HW; Prepare for a unit test if you chose the unit test for the assessment

Thursday
Your choice, you can work on a project for the unit or take a unit test on the unit. Both items can count as a test grade.
Help:http://www.sosmath.com/algebra/factor/fac02/fac02.html
HW; None

Friday
Yes, it is Friday and we look at rational expressions, with a focus on factoring polynomials.
Help:https://www.khanacademy.org/math/algebra/polynomial-factorization
HW; None

Have a great weekend!
One week to Spring Break!

Week of March 13

Algebra 1

Formula For Factoring Trinomials(when a =1)

It's always easier to understand a new concept by looking at a specific example so you might want to do that first. This formula works when 'a' is 1. In other words, we will use this approach whenever the coefficient in from of x2 is 1. (If you need help factoring trinomials when a≠1$a\ne 1$, then go here.

1. identify a,b, and c in the trinomial ax2 + bx+c
2. write down all factor pairs of c
3. identify which factor pair from the previous step sums up to b
4. Substitute factor pairs into two binomials

Example of Factoring a Trinomial

Example 1

Factor x2 + 5x + 4

Step 1

Identify a,b, and c in the trinomial 
ax2 + bx+c

a= 1
b= 5
c= 4

Step 2

Write down all factor pairs of 4 
(Note: since 5 is positive we only need to think about pairs that are either both positive or both negative. Remember a negative times a negative is a positive. As the chart on the right shows you -2*-2 is positive 4...so we do have to consider these two negative factors. This is probably easier to understand if you watch our video lesson factoring trinomials)

Step 3

identify which factor pair from the previous step sums up to c

Step 4

Substitute that factor pair into two binomials

(x +4)(x+1)

Step 5

If you'd like, you can check your work by multiplying the two binomials and verify that you get the original trinomial

Algebra 2

Assessments: Unit Project given later in the week

Monday
It is the day to write equation of the polynomial from the roots and to solve polynomials with imaginary roots and real roots combined.
Help:https://www.varsitytutors.com/hotmath/hotmath_help/topics/polynomials-with-complex-roots
HW: none

Tuesday
Happy Pi Day! We will solve circle problems all day today! The work will be polynomial roots and writing equations using the roots.
Help: http://www.piday.org/

HW; Prepare for a mini quiz, a circle problem!

Wednesday
We confirm circle problems are good and there will be a mini quiz today. You will do a great job!
Help:http://www.purplemath.com/modules/fromzero2.htm
HW; None

Thursday
It is the day to look at characteristics of polynomials
Help:https://www.youtube.com/watch?v=epR8bf5PDmc
HW: None

Friday
Happy St. Patrick's Day! We continue with characteristics today
Help:http://www.sosmath.com/algebra/factor/fac03/fac03.html
HW: None

Have a great weekend! Two weeks to Spring Break!

Week of March 6, 2017

Algebra1

Factoring A GCF From an Expression Lessons

To best understand this lesson, you should make sure you know how to find the GCF of two or more terms. To learn how, see the lesson called Finding a GCF.

3x³ + 27x² + 9x

To factor out the GCF in an expression like the one above, first find the GCF of all of the expression's terms.

3	(1, 3)
27	(1, 3, 9, 27)
9	(1, 3, 9)

GCF = 3x

Next, write the GCF on the left of a set of parentheses:

3x(               )

Next, divide each term from the original expression (3x³+27x²+9x ) by the GCF (3x), then write it in the parenthesis.

3x³ / 3x = x²
27x² / 3x = 9x
9x / 3x = 3

3x(x² + 9x + 3)

The next expression we will be factoring is shown below.

36x² - 64y⁴

To begin factoring the GCF out of the expression, find the GCF of the two terms.

36	(1, 2, 3, 4, 6, 9, 12, 18, 36)
64	(1, 2, 4, 8, 16, 32, 64)

GCF = 4

As you can see, the two terms to do not have any variables in common, therefore the GCF is simply 4.
Now write 4, the GCF, on the left of a set of parentheses.

4(               )

Now divide each term 4, the GCF, and place the result inside the parentheses.

36x² / 4 = 9x²
-64y⁴ / 4 = -16y⁴

4(9x² - 16y⁴)

ALGEBRA 2

Assessments: Quiz on Wednesday and Summative assessment next week

Monday
Hope you had a great weekend! Today, we are working  on some polynomial cards  outside the classroom with varying questions on roots and factors.  Yes, you will think on this activity.
I have two colors posted, so ask me which color is the best fit for you today.  Also, you find roots of  4th degree polynomials and missing terms polynomials.
Help:http://math.stackexchange.com/questions/12787/finding-roots-of-the-fourth-degree-polynomial-2x4-3x3-11x2-9x-15
HW; None

Tuesday
Today, we look  at the Rational Root Theorem and  find all roots of a given polynomial.  I will have practice time for you today to master this concept and you will have choices on the problems.
HW; Study for quiz
Help:https://www.khanacademy.org/math/algebra2/polynomial-functions/finding-zeros-of-polynomials/v/finding-roots-or-zeros-of-polynomial-1


Wednesday
Moving along the week, you shall shine on the formative assessment (a quiz) in class today. I will have a quiz preview first to ensure you are ready this quiz. Also, we analyze the long division process to see a connection with the polynomial, the radical and the factors.
Help:https://www.khanacademy.org/math/algebra2/arithmetic-with-polynomials/long-division-of-polynomials/v/dividing-polynomials-1
HW; None

Thursday
Almost Friday! It is the day to write the equation of a polynomial given the roots and to solve a couple of circle problems ( I created these problems, so I love them)
Help:https://www.youtube.com/watch?v=gyksK76Dg1c
HW; None

Friday
Yes, it is Friday! It is time for more circle problems today and some other polynomial cards filled with thinking questions.
Help:http://www.purplemath.com/modules/fromzero2.htm
HW; None