Foundations
What is a Function?
A function relates an input to an output.
 |
It is like a machine that has an input and an output.
And the output is related somehow to the input.
|
| f(x) |
"f(x) = ... " is the classic way of writing a function.
And there are other ways, as you will see! |
Input, Relationship, Output
We will see many ways to think about functions, but there are always three main parts:
- The input
- The relationship
- The output
Some Examples of Functions
- x2 (squaring) is a function
- x3+1 is also a function
- Sine, Cosine and Tangent are functions used in trigonometry
- and there are lots more!
But we are not going to look at specific functions ...
... instead we will look at the general idea of a function.
... instead we will look at the general idea of a function.
Names
First, it is useful to give a function a name.
The most common name is "f", but we can have other names like "g" ... or even "marmalade" if we want.
But let's use "f":

We say "f of x equals x squared"
what goes into the function is put inside parentheses () after the name of the function:
So f(x) shows us the function is called "f", and "x" goes in
And we usually see what a function does with the input:
f(x) = x2 shows us that function "f" takes "x" and squares it.
The "x" is Just a Place-Holder!
Don't get too concerned about "x", it is just there to show us where the input goes and what happens to it.
It could be anything!
So this function:
f(x) = 1 - x + x2
Is the same function as:
- f(q) = 1 - q + q2
- h(A) = 1 - A + A2
- w(θ) = 1 - θ + θ2
The variable (x, q, A, etc) is just there so we know where to put the values:
f(2) = 1 - 2 + 22 = 3
Sometimes There is No Function Name
Sometimes a function has no name, and we see something like:
y = x2
But there is still:
- an input (x)
- a relationship (squaring)
- and an output (y)
Relating
At the top we said that a function was like a machine. But a function doesn't really have belts or cogs or any moving parts - and it doesn't actually destroy what we put into it!
A function relates an input to an output.
Saying "f(4) = 16" is like saying 4 is somehow related to 16. Or 4 → 16
What Types of Things Do Functions Process?
"Numbers" seems an obvious answer, but ...
... which numbers?
For example, the tree-height function h(age) = age×20 makes no sense for an age less than zero.
| |
| ... it could also be letters ("A"→"B"), or ID codes ("A6309"→"Pass") or stranger things. | |
So we need something more powerful, and that is where sets come in:
| A set is a collection of things.
Here are some examples:
Set of even numbers: {..., -4, -2, 0, 2, 4, ...}
Set of clothes: {"hat","shirt",...} Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...} Positive multiples of 3 that are less than 10: {3, 6, 9} |
Each individual thing in the set (such as "4" or "hat") is called a member, or element.
So, a function takes elements of a set, and gives back elements of a set.
A Function is Special
But a function has special rules:
- It must work for every possible input value
- And it has only one relationship for each input value
This can be said in one definition:
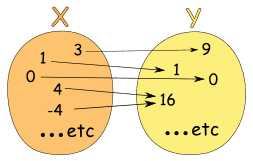
 | Formal Definition of a Function
A function relates each element of a set
with exactly one element of another set (possibly the same set). |
The Two Important Things!
1.
|
"...each element..." means that every element in X is related to some element in Y.
We say that the function covers X (relates every element of it).
(But some elements of Y might not be related to at all, which is fine.)
|
2.
|
"...exactly one..." means that a function is single valued. It will not give back 2 or more results for the same input.
So "f(2) = 7 or 9" is not right!
|
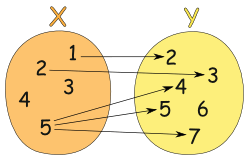
Note: "One-to-many" is not allowed, but "many-to-one" is allowed:
| ||
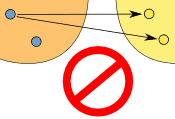 | 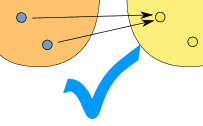 | |
| (one-to-many) | (many-to-one) | |
| This is NOT OK in a function | But this is OK in a function | |
When a relationship does not follow those two rules then it is not a function ... it is still a relationship, just not a function.

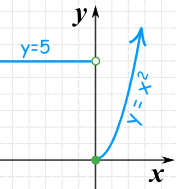
Vertical Line Test
On a graph, the idea of single valued means that no vertical line ever crosses more than one value.
If it crosses more than once it is still a valid curve, but is not a function.
Some types of functions have stricter rules, to find out more you can read Injective, Surjective and Bijective
Infinitely Many
My examples have just a few values, but functions usually work on sets with infinitely many elements.
Domain, Codomain and Range
In our examples above
- the set "X" is called the Domain,
- the set "Y" is called the Codomain, and
- the set of elements that get pointed to in Y (the actual values produced by the function) is called the Range.
We have a special page on Domain, Range and Codomain if you want to know more.
So Many Names!
Functions have been used in mathematics for a very long time, and lots of different names and ways of writing functions have come about.
Here are some common terms you should get familiar with:

Ordered Pairs
And here is another way to think about functions:
Write the input and output of a function as an "ordered pair", such as (4,16).
They are called ordered pairs because the input always comes first, and the output second:
(input, output)
So it looks like this:
( x, f(x) )
Set of Ordered Pairs
A function can then be defined as a set of ordered pairs:
But the function has to be single valued, so we also say
"if it contains (a, b) and (a, c), then b must equal c"
Which is just a way of saying that an input of "a" cannot produce two different results.
 | A Benefit of Ordered Pairs
We can graph them...
... because they are also coordinates!
So a set of coordinates is also a function (if they follow
the rules above, that is) |
A Function Can be in Pieces
We can create functions that behave differently depending on the input value
Read more at Piecewise Functions.
Explicit vs Implicit
One last topic: the terms "explicit" and "implicit".
"Explicit" is when the function shows us how to go directly from x to y, such as:
y = x3 - 3
When we know x, we can find y
That is the classic y = f(x) style.
"Implicit" is when it is not given directly such as:
x2 - 3xy + y3 = 0
When we know x, how do we find y?
It may be hard (or impossible!) to go directly from x to y.
"Implicit" comes from "implied", in other words shown indirectly.
Graphing
- The Function Grapher can only handle explicit functions,
- The Equation Grapher can handle both types (but takes a little longer, and sometimes gets it wrong).
Conclusion
- a function relates inputs to outputs
- a function takes elements from a set (the domain) and relates them to elements in a set (the codomain).
- all the outputs (the actual values related to) are together called the range
- a function is a special type of relation where:
- every element in the domain is included, and
- any input produces only one output (not this or that)
- an input and its matching output are together called an ordered pair
- so a function can also be seen as a set of ordered pairs
https://www.mathsisfun.com/sets/function.html
Anatomy
An Overview of Blood
Recall that blood is a connective tissue. Like all connective tissues, it is made up of cellular elements and an extracellular matrix. The cellular elements—referred to as the formed elements—include red blood cells (RBCs), white blood cells (WBCs), and cell fragments called platelets. The extracellular matrix, called plasma, makes blood unique among connective tissues because it is fluid. This fluid, which is mostly water, perpetually suspends the formed elements and enables them to circulate throughout the body within the cardiovascular system.
Functions of Blood
The primary function of blood is to deliver oxygen and nutrients to and remove wastes from body cells, but that is only the beginning of the story. The specific functions of blood also include defense, distribution of heat, and maintenance of homeostasis.
Transportation
Nutrients from the foods you eat are absorbed in the digestive tract. Most of these travel in the bloodstream directly to the liver, where they are processed and released back into the bloodstream for delivery to body cells. Oxygen from the air you breathe diffuses into the blood, which moves from the lungs to the heart, which then pumps it out to the rest of the body. Moreover, endocrine glands scattered throughout the body release their products, called hormones, into the bloodstream, which carries them to distant target cells. Blood also picks up cellular wastes and byproducts, and transports them to various organs for removal. For instance, blood moves carbon dioxide to the lungs for exhalation from the body, and various waste products are transported to the kidneys and liver for excretion from the body in the form of urine or bile.
Defense
Many types of WBCs protect the body from external threats, such as disease-causing bacteria that have entered the bloodstream in a wound. Other WBCs seek out and destroy internal threats, such as cells with mutated DNA that could multiply to become cancerous, or body cells infected with viruses.
When damage to the vessels results in bleeding, blood platelets and certain proteins dissolved in the plasma, the fluid portion of the blood, interact to block the ruptured areas of the blood vessels involved. This protects the body from further blood loss.
Maintenance of Homeostasis
Recall that body temperature is regulated via a classic negative-feedback loop. If you were exercising on a warm day, your rising core body temperature would trigger several homeostatic mechanisms, including increased transport of blood from your core to your body periphery, which is typically cooler. As blood passes through the vessels of the skin, heat would be dissipated to the environment, and the blood returning to your body core would be cooler. In contrast, on a cold day, blood is diverted away from the skin to maintain a warmer body core. In extreme cases, this may result in frostbite.
Blood also helps to maintain the chemical balance of the body. Proteins and other compounds in blood act as buffers, which thereby help to regulate the pH of body tissues. Blood also helps to regulate the water content of body cells.
Composition of Blood
You have probably had blood drawn from a superficial vein in your arm, which was then sent to a lab for analysis. Some of the most common blood tests—for instance, those measuring lipid or glucose levels in plasma—determine which substances are present within blood and in what quantities. Other blood tests check for the composition of the blood itself, including the quantities and types of formed elements.
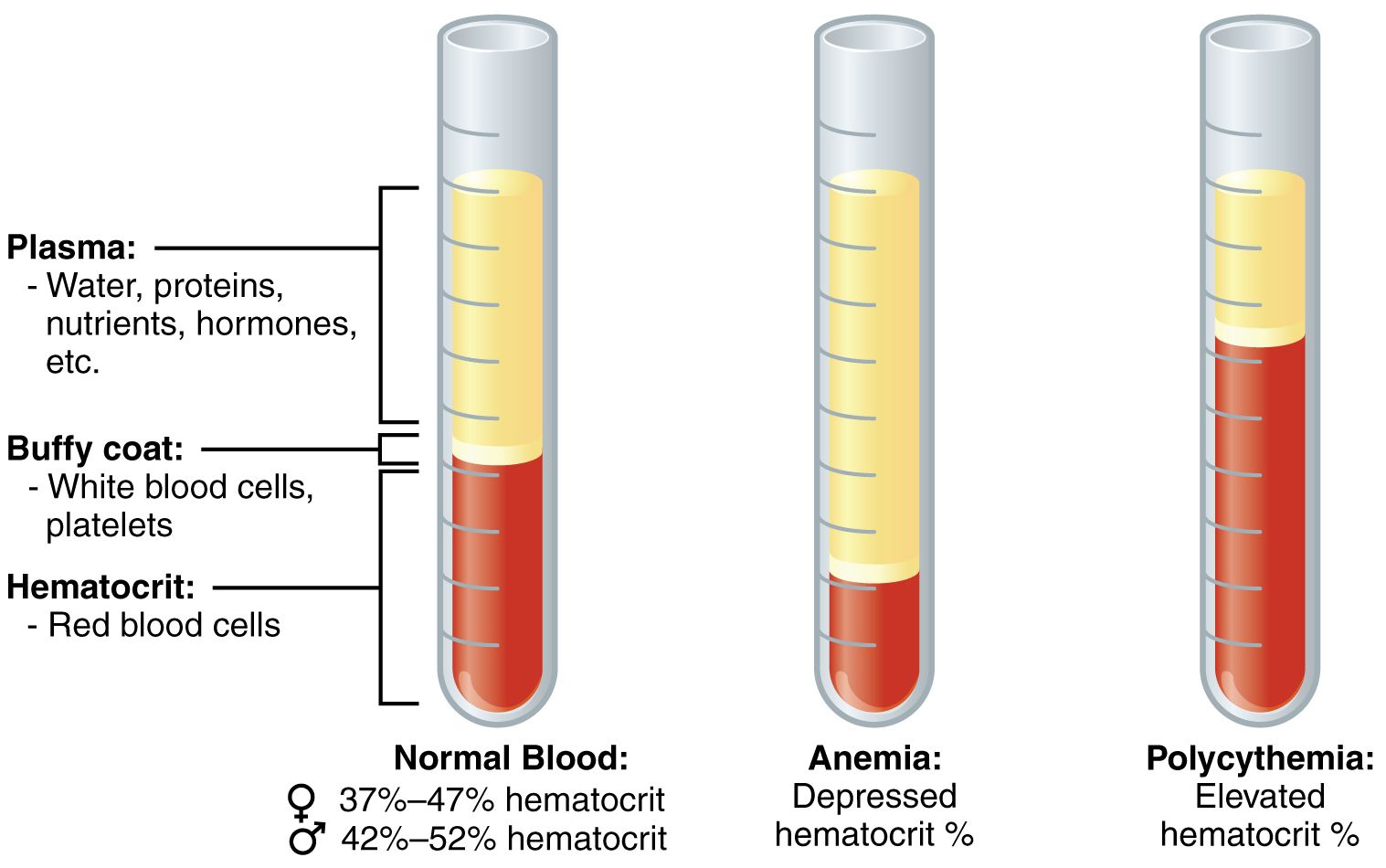
One such test, called a hematocrit, measures the percentage of RBCs, clinically known as erythrocytes, in a blood sample. It is performed by spinning the blood sample in a specialized centrifuge, a process that causes the heavier elements suspended within the blood sample to separate from the lightweight, liquid plasma ([link]). Because the heaviest elements in blood are the erythrocytes, these settle at the very bottom of the hematocrit tube. Located above the erythrocytes is a pale, thin layer composed of the remaining formed elements of blood. These are the WBCs, clinically known as leukocytes, and the platelets, cell fragments also called thrombocytes. This layer is referred to as the buffy coat because of its color; it normally constitutes less than 1 percent of a blood sample. Above the buffy coat is the blood plasma, normally a pale, straw-colored fluid, which constitutes the remainder of the sample.
The volume of erythrocytes after centrifugation is also commonly referred to as packed cell volume (PCV). In normal blood, about 45 percent of a sample is erythrocytes. The hematocrit of any one sample can vary significantly, however, about 36–50 percent, according to gender and other factors. Normal hematocrit values for females range from 37 to 47, with a mean value of 41; for males, hematocrit ranges from 42 to 52, with a mean of 47. The percentage of other formed elements, the WBCs and platelets, is extremely small so it is not normally considered with the hematocrit. So the mean plasma percentage is the percent of blood that is not erythrocytes: for females, it is approximately 59 (or 100 minus 41), and for males, it is approximately 53 (or 100 minus 47).
Composition of Blood
Characteristics of Blood
When you think about blood, the first characteristic that probably comes to mind is its color. Blood that has just taken up oxygen in the lungs is bright red, and blood that has released oxygen in the tissues is a more dusky red. This is because hemoglobin is a pigment that changes color, depending upon the degree of oxygen saturation.
Blood is viscous and somewhat sticky to the touch. It has a viscosity approximately five times greater than water. Viscosity is a measure of a fluid’s thickness or resistance to flow, and is influenced by the presence of the plasma proteins and formed elements within the blood. The viscosity of blood has a dramatic impact on blood pressure and flow. Consider the difference in flow between water and honey. The more viscous honey would demonstrate a greater resistance to flow than the less viscous water. The same principle applies to blood.
The normal temperature of blood is slightly higher than normal body temperature—about 38 °C (or 100.4 °F), compared to 37 °C (or 98.6 °F) for an internal body temperature reading, although daily variations of 0.5 °C are normal. Although the surface of blood vessels is relatively smooth, as blood flows through them, it experiences some friction and resistance, especially as vessels age and lose their elasticity, thereby producing heat. This accounts for its slightly higher temperature.
The pH of blood averages about 7.4; however, it can range from 7.35 to 7.45 in a healthy person. Blood is therefore somewhat more basic (alkaline) on a chemical scale than pure water, which has a pH of 7.0. Blood contains numerous buffers that actually help to regulate pH.
Blood constitutes approximately 8 percent of adult body weight. Adult males typically average about 5 to 6 liters of blood. Females average 4–5 liters.
Blood Plasma
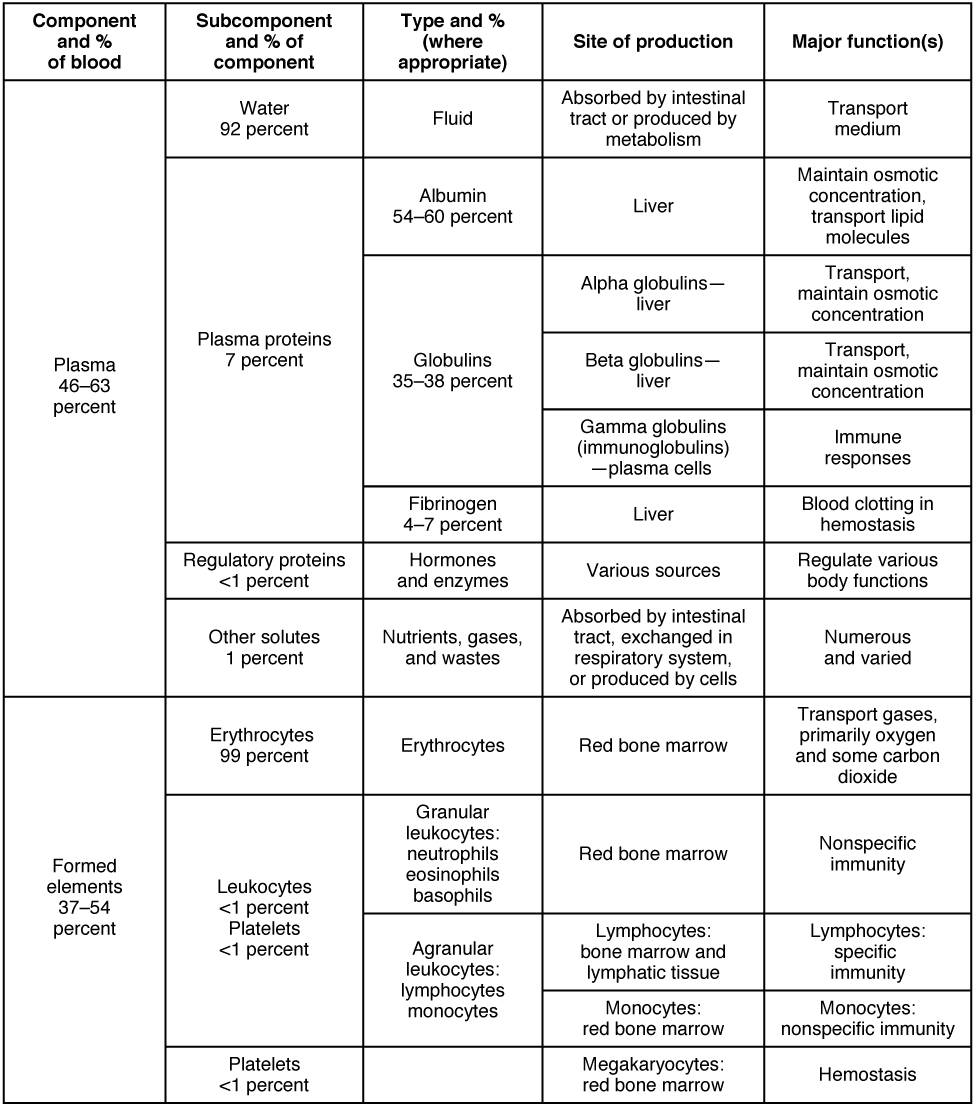
Like other fluids in the body, plasma is composed primarily of water: In fact, it is about 92 percent water. Dissolved or suspended within this water is a mixture of substances, most of which are proteins. There are literally hundreds of substances dissolved or suspended in the plasma, although many of them are found only in very small quantities.
Visit this site for a list of normal levels established for many of the substances found in a sample of blood. Serum, one of the specimen types included, refers to a sample of plasma after clotting factors have been removed. What types of measurements are given for levels of glucose in the blood?
Plasma Proteins
About 7 percent of the volume of plasma—nearly all that is not water—is made of proteins. These include several plasma proteins (proteins that are unique to the plasma), plus a much smaller number of regulatory proteins, including enzymes and some hormones. The major components of plasma are summarized in [link].
The three major groups of plasma proteins are as follows:
- Albumin is the most abundant of the plasma proteins. Manufactured by the liver, albumin molecules serve as binding proteins—transport vehicles for fatty acids and steroid hormones. Recall that lipids are hydrophobic; however, their binding to albumin enables their transport in the watery plasma. Albumin is also the most significant contributor to the osmotic pressure of blood; that is, its presence holds water inside the blood vessels and draws water from the tissues, across blood vessel walls, and into the bloodstream. This in turn helps to maintain both blood volume and blood pressure. Albumin normally accounts for approximately 54 percent of the total plasma protein content, in clinical levels of 3.5–5.0 g/dL blood.
- The second most common plasma proteins are the globulins. A heterogeneous group, there are three main subgroups known as alpha, beta, and gamma globulins. The alpha and beta globulins transport iron, lipids, and the fat-soluble vitamins A, D, E, and K to the cells; like albumin, they also contribute to osmotic pressure. The gamma globulins are proteins involved in immunity and are better known as an antibodies or immunoglobulins. Although other plasma proteins are produced by the liver, immunoglobulins are produced by specialized leukocytes known as plasma cells. (Seek additional content for more information about immunoglobulins.) Globulins make up approximately 38 percent of the total plasma protein volume, in clinical levels of 1.0–1.5 g/dL blood.
- The least abundant plasma protein is fibrinogen. Like albumin and the alpha and beta globulins, fibrinogen is produced by the liver. It is essential for blood clotting, a process described later in this chapter. Fibrinogen accounts for about 7 percent of the total plasma protein volume, in clinical levels of 0.2–0.45 g/dL blood.
Other Plasma Solutes
In addition to proteins, plasma contains a wide variety of other substances. These include various electrolytes, such as sodium, potassium, and calcium ions; dissolved gases, such as oxygen, carbon dioxide, and nitrogen; various organic nutrients, such as vitamins, lipids, glucose, and amino acids; and metabolic wastes. All of these nonprotein solutes combined contribute approximately 1 percent to the total volume of plasma.
CAREER CONNECTION
Phlebotomy and Medical Lab TechnologyPhlebotomists are professionals trained to draw blood (phleb- = “a blood vessel”; -tomy = “to cut”). When more than a few drops of blood are required, phlebotomists perform a venipuncture, typically of a surface vein in the arm. They perform a capillary stick on a finger, an earlobe, or the heel of an infant when only a small quantity of blood is required. An arterial stick is collected from an artery and used to analyze blood gases. After collection, the blood may be analyzed by medical laboratories or perhaps used for transfusions, donations, or research. While many allied health professionals practice phlebotomy, the American Society of Phlebotomy Technicians issues certificates to individuals passing a national examination, and some large labs and hospitals hire individuals expressly for their skill in phlebotomy.
Medical or clinical laboratories employ a variety of individuals in technical positions:
- Medical technologists (MT), also known as clinical laboratory technologists (CLT), typically hold a bachelor’s degree and certification from an accredited training program. They perform a wide variety of tests on various body fluids, including blood. The information they provide is essential to the primary care providers in determining a diagnosis and in monitoring the course of a disease and response to treatment.
- Medical laboratory technicians (MLT) typically have an associate’s degree but may perform duties similar to those of an MT.
- Medical laboratory assistants (MLA) spend the majority of their time processing samples and carrying out routine assignments within the lab. Clinical training is required, but a degree may not be essential to obtaining a position.
- http://philschatz.com/anatomy-book/contents/m46691.html
Geometry
Coordinate Proof
Essential Question: How are the slope and the distance formula used to determine properties of polygons and circles?
Lesson
A figure in a coordinate plane may appear to be one of the familiar quadrilaterals, but proof is needed to show that the figure meets the definition of the particular shape. The slope formula and distance formula can be used to prove properties of quadrilaterals and to classify them.
Slope of a Line
The slope of a non-vertical line can be found using the formula below. The slope of a vertical line is undefined.


m(AB) is used to denote the slope of line segment AB.
For instance, find the slope of the line between (-3, 5) and (2, 1).

Distance Between Two Points
The distance between two points can be found using the formula below.

For instance, find the distance between (-2, 5) and (3, -1).

Perpendicular and Parallel Lines
To show that two lines are parallel, show that their slopes are equal.
To show that two lines are perpendicular (form a right angle), show that the product of their slopes is -1 (the slopes are opposite reciprocals). The symbol for perpendicular is ┴.
To show that two lines are congruent, show that they have equal measure (equal length) by using the distance formula.
Proving Quadrilaterals
To prove a quadrilateral is a parallelogram:
Show that both pairs of opposite sides are parallel.
Show that both pairs of opposite sides are congruent.
Show that both pairs of opposite sides are parallel.
Show that both pairs of opposite sides are congruent.
To prove a quadrilateral is a rhombus:
Show that all four sides are congruent.
Show that all four sides are congruent.
To prove a quadrilateral is a rectangle:
First show it is a parallelogram by showing that both pairs of opposite sides are parallel, and then show that one angle is a right angle (the other 3 angles will be right angles due to other properties of parallelograms).
Show that all four angles are right angles.
First show it is a parallelogram by showing that both pairs of opposite sides are parallel, and then show that one angle is a right angle (the other 3 angles will be right angles due to other properties of parallelograms).
Show that all four angles are right angles.
To prove a quadrilateral is a square:
First show it is a rhombus by proving that all sides are congruent, and then show it is a rectangle by showing that one angle is a right angle.
First show it is a rhombus by proving that all sides are congruent, and then show it is a rectangle by showing that one angle is a right angle.
To prove a quadrilateral is a kite:
Show that it has two pairs of consecutive sides congruent, but NOT all four sides congruent.
Show that it has two pairs of consecutive sides congruent, but NOT all four sides congruent.
To prove a quadrilateral is a trapezoid:
Show it has exactly one pair of sides parallel. The other pair must be shown to not be parallel, so all four slopes need to be computed.
Show it has exactly one pair of sides parallel. The other pair must be shown to not be parallel, so all four slopes need to be computed.
To prove a quadrilateral is an isosceles trapezoid:
First, show it is a trapezoid, and then show it has exactly one pair of congruent sides (the non-parallel sides).
First, show it is a trapezoid, and then show it has exactly one pair of congruent sides (the non-parallel sides).
To prove a triangle is a right triangle:
Show that one angle is a right angle.
Show that one angle is a right angle.
Prove a point is on a circle:
A circle is a set of points equidistant from a given point called the center of the circle. To prove a point in on a circle, prove that the distance from the given point to the center is equal to the radius of the circle. The radius is the segment that connects the center to any point on the circle.
A circle is a set of points equidistant from a given point called the center of the circle. To prove a point in on a circle, prove that the distance from the given point to the center is equal to the radius of the circle. The radius is the segment that connects the center to any point on the circle.
Examples
Example 1. Prove that quadrilateral A (1, 2), B (2, 5), C (5, 7) D (4, 4) is a parallelogram using slopes.
Solution: First, plot the points and sketch the figure. By definition, a parallelogram is a quadrilateral with two pairs of parallel sides. Verify the figure is a parallelogram by computing the slopes. The slopes of the opposite sides should be equal.

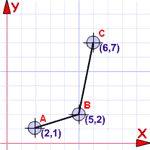
Example 2. Prove that (1, 1), (4, 4) and (6, 2) are the vertices of a right triangle.
Solution: First, plot the points and sketch the figure. The angle that appears to be the right angle is ∠B. Prove that ∠B is the right angle by determining the slopes of the two lines that make up angle B, line segments AB and BC.

Example 3. Prove that A (-3, 2), B (-2, 6), C (2, 7), D (1, 3) is a rhombus.
Solution: First, plot the points and sketch the figure. The angles do not appear to be right angles so the figure is not a square, there is no need to compute the slopes. Verify the figure is a rhombus by determining the lengths of all four sides. If they are congruent, the figure is a rhombus.

Since all sides measure √17, BA = DC = CB = DA. ABCD is a rhombus because all four sides are congruent.
Example 4. A (-4, 0), B (3, 0), and C (2, -5) represent three points of a parallelogram ABCD. Determine the coordinates of point D.
Solution: Graph the points. There are three different points that would combine with the given points to create a parallelogram, as shown in the second graph. When labeling a figure, vertices must go in order either clockwise or counter-clockwise. The only point that could be point D is (-5, -5).