Week of April 24, 2017

ALGEBRA 1 Exponential Functions: Introduction Exponential functions look somewhat similar to functions you have seen before, in that they involve exponents, but there is a big difference, in that the variable is now the power, rather than the base. Previously, you have dealt with such functions as f(x) = x2, where the variable x was the base and the number 2 was the power. In the case of exponentials, however, you will be dealing with functions such as g(x) = 2x, where the base is the fixed number, and the power is the variable. Let's look more closely at the function g(x) = 2x. To evaluate this function, we operate as usual, picking values of x, plugging them in, and simplifying for the answers. But to evaluate 2x, we need to remember how exponents work. In particular, we need to remember that negative exponents mean "put the base on the other side of the fraction line". So, while positive x-values give us values like these:         ...negative x-values give us values like these:     Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved          Putting together the "reasonable" (nicely graphable) points, this is our T-chart:         ...and this is our graph:      Exponential growth is "bigger" and "faster" than polynomial growth. This means that, no matter what the degree is on a given polynomial, a given exponential function will eventually be bigger than the polynomial. Even though the exponential function may start out really, really small, it will eventually overtake the growth of the polynomial, since it doubles all the time.    For instance, x10 seems much "bigger" than 10x, and initially it is:          But eventually 10x (in blue below) catches up and overtakes x10 (at the red circle below, where x is ten and y is ten billion), and it's "bigger" than x10 forever after:          Exponential functions always have some positive number other than 1 as the base. If you think about it, having a negative number (such as –2) as the base wouldn't be very useful, since the even powers would give you positive answers (such as "(–2)2 = 4") and the odd powers would give you negative answers (such as "(–2)3 = –8"), and what would you even do with the powers that aren't whole numbers? Also, having 0 or 1 as the base would be kind of dumb, since 0 and 1 to any power are just 0 and 1, respectively; what would be the point? This is why exponentials always have something positive and other than 1 as the base. Source:http://www.purplemath.com/modules/expofcns.htm ALGEBRA 2 Monday Today, we look at the more advanced rational equations, be ready to use FOIL. Help:http://www.purplemath.com/modules/solverad.htm HW; None Tuesday It is time to look at the combination of rational equations, all types on one page and to review for the test. Help:https://www.khanacademy.org/math/algebra2/radical-equations-and-functions/solving-square-root-equations/v/solving-radical-equations HW: ( 1st) Study for test and finish the review sheet ( 3rd) None Wednesday 1st- test day, be ready 3rd- prepare for test on Thursday Help:https://www.mathsisfun.com/algebra/radical-equations-solving.html HW ( 3rd ) study for the test and review sheet Thursday 3rd - test day! You shall shine! HW; None Friday It is prom tonight and I will not be in class. I will leave practice sheets for you to do or you can work on makeup work. HW; None Help: N/A See you on Monday Have a great weekend!

Week of April 17,2017

Algebra1

The Quadratic Formula

Often, the simplest way to solve "ax2 + bx + c = 0" for the value of x is to factor the quadratic, set each factor equal to zero, and then solve each factor. But sometimes the quadratic is too messy, or it doesn't factor at all, or you just don't feel like factoring. While factoring may not always be successful, the Quadratic Formula can always find the solution.

The Quadratic Formula uses the "a", "b", and "c" from "ax2+ bx + c", where "a", "b", and "c" are just numbers; they are the "numerical coefficients" of the quadratic equation they've given you to solve.

The Quadratic Formula is derived from the process of completing the square, and is formally stated as:

The Quadratic Formula: For ax2 + bx + c = 0, the values of x which are the solutions of the equation are given by:

$x = \dfrac{-b \pm\sqrt{b^2 - 4ac\,}}{2a}$

For the Quadratic Formula to work, you must have your equation arranged in the form "(quadratic) = 0". Also, the "2a" in the denominator of the Formula is underneath everything above, not just the square root. And it's a "2a" under there, not just a plain "2". Make sure that you are careful not to drop the square root or the "plus/minus" in the middle of your calculations, or I can guarantee that you will forget to "put them back in" on your test, and you'll mess yourself up. Remember that "b2" means "the square of ALL of b, including its sign", so don't leave b2 being negative, even if b is negative, because the square of a negative is a positive.

In other words, don't be sloppy and don't try to take shortcuts, because it will only hurt you in the long run. Trust me on this!

Here are some examples of how the Quadratic Formula works:

• Solve x2 + 3x – 4 = 0

This quadratic happens to factor:

x2 + 3x – 4 = (x + 4)(x – 1) = 0

...so I already know that the solutions are x = –4 and x = 1. How would my solution look in the Quadratic Formula? Using a = 1, b = 3, and c = –4, my solution looks like this:

$x = \dfrac{-(3) \pm \sqrt{(3)^2 - 4(1)(-4)\,}}{2(1)}$

$= \dfrac{-3 \pm \sqrt{9 + 16\,}}{2} = \dfrac{-3 \pm \sqrt{25\,}}{2}$

$= \dfrac{-3 \pm 5}{2} = \dfrac{-3 - 5}{2},\, \dfrac{-3 + 5}{2}$

$= \dfrac{-8}{2},\, \dfrac{2}{2} = -4,\, 1$

Then, as expected, the solution is x = –4, x = 1.

Algebra 2

Assessments: Unit 4 test is Tuesday

Monday
We are reviewing rational expressions  and equations for a test.
Help:https://www.khanacademy.org/math/algebra2/rational-expressions-equations-and-functions
HW; Review sheet

Tuesday
Test day, you shall shine!
Help:http://www.purplemath.com/modules/solvrtnl.htm
HW; None

Wednesday
 You can wrap up the test today, write on rational expressions and we look at basic radical equations
Help:https://www.khanacademy.org/math/algebra2/radical-equations-and-functions/solving-square-root-equations/v/solving-radical-equations
HW; None

Thursday
It is day two of radical equations!
Help:http://www.mathplanet.com/education/algebra-1/radical-expressions/radical-equations
HW; None

Friday
Yes, it is Friday!
Day three of radical equations with radicals on both sides.
Help:https://www.mathsisfun.com/algebra/radical-equations-solving.html
HW; None


Have a great weekend!

Week of April 10, 2017

Welcome back from spring break!

Tutoring: See me for times as schedule is not set for the week

Assessments: Test is likely on Friday

Monday
Welcome back from break! Today, we look at your heartrate and the medicine problem.
Help: ( not much on the web here)
HW;  None

Tuesday
Today, we look at the building problem and the TV problem.
Help:http://www.metric-conversions.org/length/feet-to-meters.htm
HW; None

Wednesday
It is TV problem day two.
Help:https://www.quora.com/How-does-one-calculate-a-televisions-height-and-width-based-on-its-diagonal-length-and-aspect-ratio
HW; None

Thursday
Review day!
Help:http://www.metric-conversions.org/
HW; Study for test

Friday
Test day!
HW; None

Have a great weekend!
Ms. Harrell

Week of 04.10.2017-04.14.2017 Algebra 2

Tutoring: Tuesday afternoon

Assessments: Unit test is Friday

Monday
Welcome back from break! Today, we  look at add and subtract rational expressions
Help:http://www.mesacc.edu/~scotz47781/mat120/notes/rational/add_subtract/add_subtract.html
HW; None


Tuesday
It is rational equations today
Help:http://www.purplemath.com/modules/solvrtnl.htm
HW; None


Wednesday
It is rational equations day two  today, be ready to find the LCD of all 3 denominators and applications.
Help:https://www.youtube.com/watch?v=Y6x06SBbEcA
HW; None


Thursday
It is  application wrap up and review day.
Help:https://www.khanacademy.org/math/algebra2/rational-expressions-equations-and-functions/modeling-with-rational-functions/v/applying-rational-equations-1
HW; None


Friday
Test day!
Help:http://tutorial.math.lamar.edu/Classes/Alg/RationalExpressions.aspx

HW; None


Algebra 1

Transform means change, and these transformations change the simple quadratic $y=x^2$y=x2 into other quadratics by moving (translations), flipping (reflecting) and making the graph appear more or less steep (dilating).

By using the above applet, step through these instructions.

• Start with the simple quadratic $y=x^2$y=x2
• Dilate the quadratic by factor of $2$2.
• Reflect on the $x$x axis
• Translate vertically by $2$2 and horizontally by $-3$−3 units.  

How has the graph changed? Can you visualize the changes without using the applet?  What is the resulting equation?

Equations and Transformations of Quadratics

Transformations of quadratics will change the equation of the quadratic.  Here are some of the most common types of quadratic equations, and what they mean with regards to the transformations that have occurred.  

$y=ax^2$y=ax2

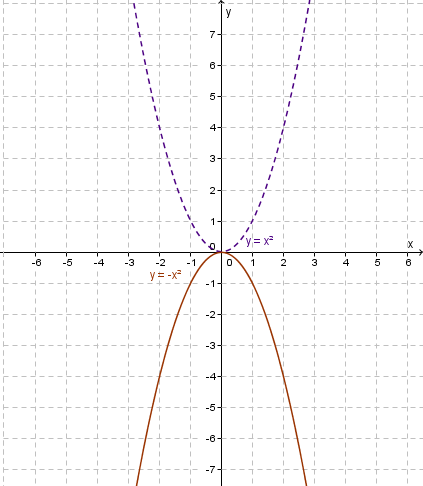
 If $a<0$a<0 (that is $a$a is negative) then we have a reflection parallel to the $x$x axis.  It's like the quadratic has been flipped upside down.

Shows the reflection of 

$y=x^2$y=x2 to $y=-x^2$y=−x2

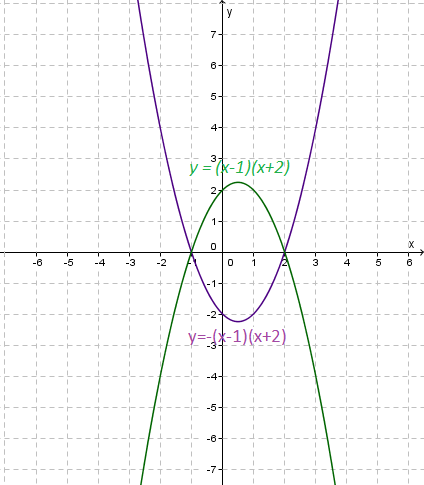
Shows the reflection of 

$y=\left(x-1\right)\left(x+2\right)$y=(x−1)(x+2) to $y=-\left(x-1\right)\left(x+2\right)$y=−(x−1)(x+2)

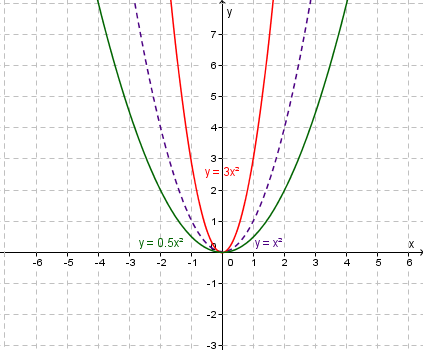
$y=ax^2$y=ax2

 

This is a quadratic that has been dilated vertically by a factor of $a$a  

If $\left|a\right|>1$|a|>1 then the graph is steeper than $y=x^2$y=x2

If  $\left|a\right|<1$|a|<1 then the graph is flatter than $y=x^2$y=x2. 

Dilation of $y=x^2$y=x2 to $y=3x^2$y=3x2 and $y=\frac{1}{2}x^2$y=12 x2

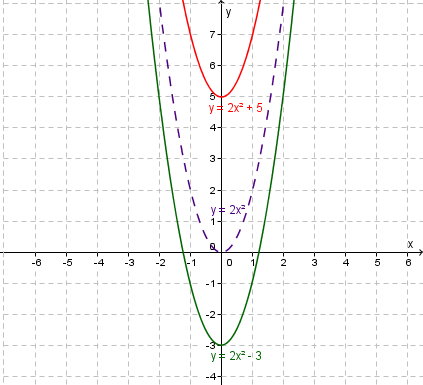
$y=ax^2+k$y=ax2+k

In the graph $y=ax^2+k$y=ax2+k, the quadratic has been vertically translated by $k$k units.  

If $k>0$k>0 then the translation is up.

If $k<0$k<0 then the translation is down.

Vertical translation.  

Showing one curve $y=2x^2+5$y=2x2+5 having a vertical translation of up $5$5 units, and

another $y=2x^2-3$y=2x2−3 having a vertical translation of down $3$3 units.

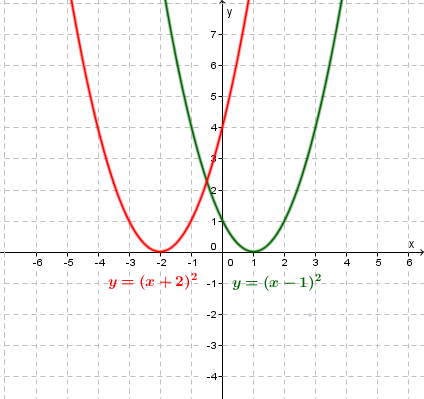
$y=\left(x-h\right)^2$y=(x−h)2

The $h$h indicates the horizontal translation.  

If $h>0$h>0, that is the factor in the parentheses is $\left(x-h\right)$(x−h) than we have a horizontal translation of $h$h units right.

If $h<0$h<0 , that is the factor in the parentheses is $\left(x--h\right)=\left(x+h\right)$(x−−h)=(x+h) than we have a horizontal translations of $h$h units left.  

The graph $y=x^2$y=x2 being horizontally translated $2$2 units left

to $y=\left(x+2\right)^2$y=(x+2)2 and $1$1 unit right to $y=\left(x-1\right)^2$y=(x−1)2

Source: https://mathspace.co