Foundations:
Complete unit homework packet.
Anatomy:
Muscle packet is due tomorrow.
Geometry:
3.1 and 3.2 quiz is tomorrow. Unit test is on Friday 9/22.
http://www.mathwarehouse.com/trigonometry/sine-cosine-tangent-practice3.php
Problem: Ms. Jensen likes to divide her class into groups of 2. Use mathematical symbols to represent all the students in her class.
Solution: Let g represent the number of groups in Ms. Jensen's class.
Then 2 · g, or 2g can represent "g groups of 2 students".
In the problem above, the variable g represents the number of groups in Ms. Jensen's class. A variable is a symbol used to represent a number in an expression or an equation. The value of this number can vary (change). Let's look at an example in which we use a variable.
Example 1: Write each phrase as a mathematical expression.
| Phrase | Expression |
| the sum of nine and eight | 9 + 8 |
| the sum of nine and a number x | 9 + x |
The expression 9 + 8 represents a single number (17). This expression is a numerical expression, (also called an arithmetic expression). The expression 9 + x represents a value that can change. If x is 2, then the expression 9 + x has a value of 11. If x is 6, then the expression has a value of 15. So 9 + x is an algebraic expression. In the next few examples, we will be working solely with algebraic expressions.
Example 2: Write each phrase as an algebraic expression.
| Phrase | Expression |
| nine increased by a number x | 9 + x |
| fourteen decreased by a number p | 14 - p |
| seven less than a number t | t - 7 |
| the product of 9 and a number n | 9 · n or 9n |
| thirty-two divided by a number y | 32 ÷ y or  |
In Example 2, each algebraic expression consisted of one number, one operation and one variable. Let's look at an example in which the expression consists of more than one number and/or operation.
Example 3: Write each phrase as an algebraic expression using the variable n.
| Phrase | Expression |
| five more than twice a number | 2n + 5 |
| the product of a number and 6 | 6n |
| seven divided by twice a number | 7 ÷ 2n or  |
| three times a number decreased by 11 | 3n - 11 |
Anatomy
Anatomical motions
What motions involve increasing or decreasing the angle of the foot at the ankle?
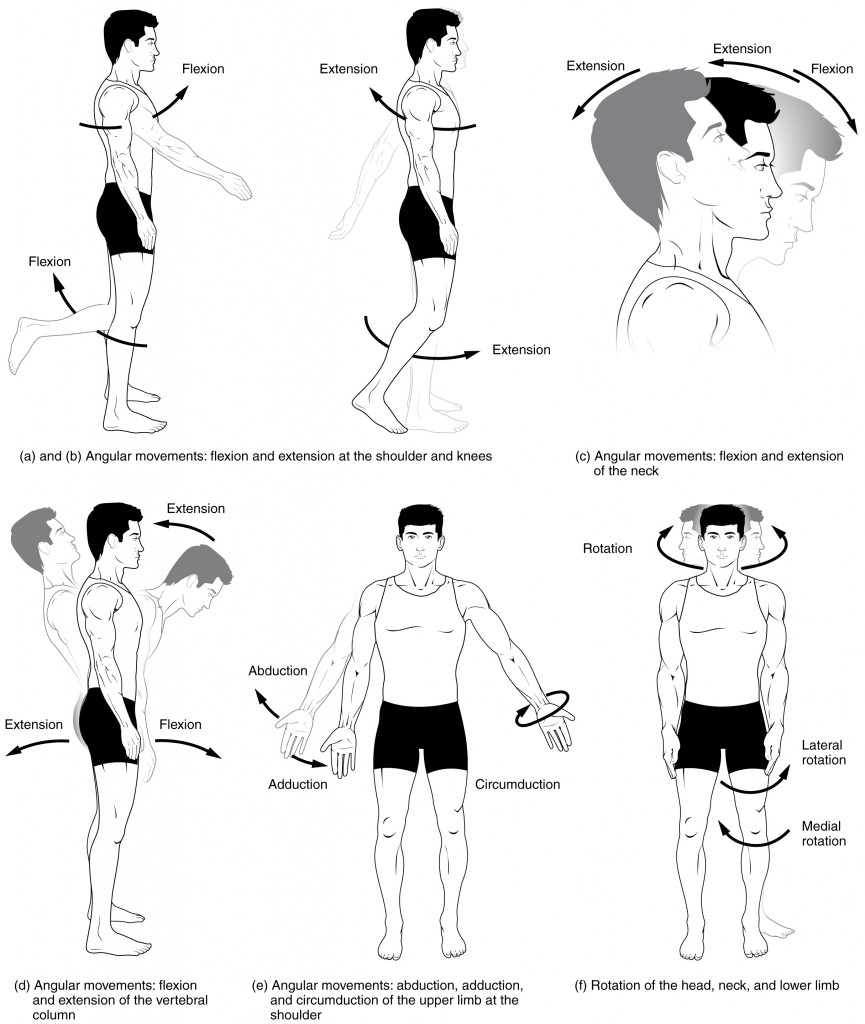
Figure 1. Movements of the Body, Part 1. Synovial joints give the body many ways in which to move. (a)–(b) Flexion and extension motions are in the sagittal (anterior–posterior) plane of motion. These movements take place at the shoulder, hip, elbow, knee, wrist, metacarpophalangeal, metatarsophalangeal, and interphalangeal joints. (c)–(d) Anterior bending of the head or vertebral column is flexion, while any posterior-going movement is extension. (e) Abduction and adduction are motions of the limbs, hand, fingers, or toes in the coronal (medial–lateral) plane of movement. Moving the limb or hand laterally away from the body, or spreading the fingers or toes, is abduction. Adduction brings the limb or hand toward or across the midline of the body, or brings the fingers or toes together. Circumduction is the movement of the limb, hand, or fingers in a circular pattern, using the sequential combination of flexion, adduction, extension, and abduction motions. Adduction/abduction and circumduction take place at the shoulder, hip, wrist, metacarpophalangeal, and metatarsophalangeal joints. (f) Turning of the head side to side or twisting of the body is rotation. Medial and lateral rotation of the upper limb at the shoulder or lower limb at the hip involves turning the anterior surface of the limb toward the midline of the body (medial or internal rotation) or away from the midline (lateral or external rotation).
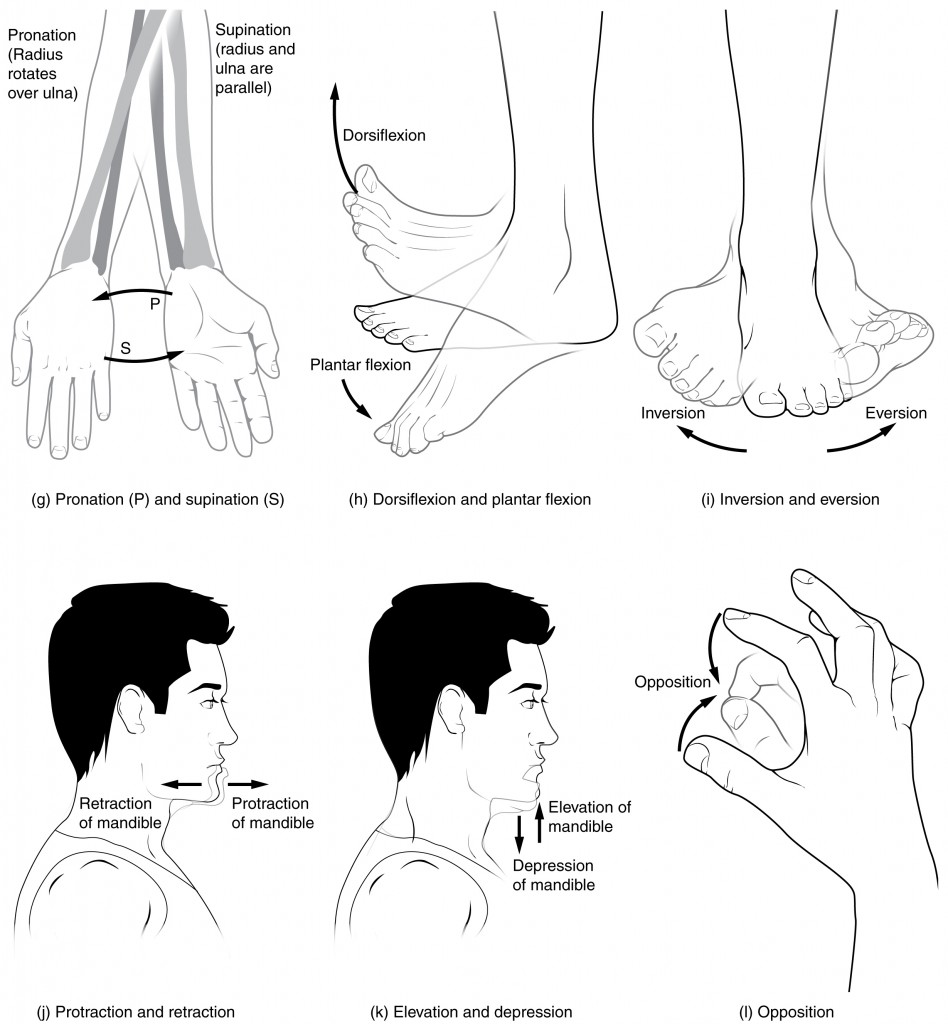
Figure 2. Movements of the Body, Part 2. (g) Supination of the forearm turns the hand to the palm forward position in which the radius and ulna are parallel, while forearm pronation turns the hand to the palm backward position in which the radius crosses over the ulna to form an “X.” (h) Dorsiflexion of the foot at the ankle joint moves the top of the foot toward the leg, while plantar flexion lifts the heel and points the toes. (i) Eversion of the foot moves the bottom (sole) of the foot away from the midline of the body, while foot inversion faces the sole toward the midline. (j) Protraction of the mandible pushes the chin forward, and retraction pulls the chin back. (k) Depression of the mandible opens the mouth, while elevation closes it. (l) Opposition of the thumb brings the tip of the thumb into contact with the tip of the fingers of the same hand and reposition brings the thumb back next to the index finger.
Geometry
Properties of Equality (for proving algebraic expressions)