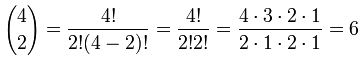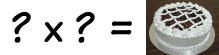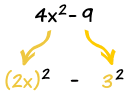Week of August 26, 2019

Open House

Tomorrow 8/17/19 @ 6.p.m.

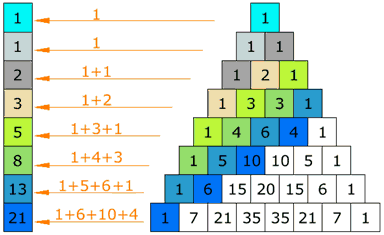
Pascal's Triangle

One of the most interesting Number Patterns is Pascal's Triangle (named after Blaise Pascal, a famous French Mathematician and Philosopher).

To build the triangle, start with "1" at the top, then continue placing numbers below it in a triangular pattern. 

Each number is the numbers directly above it added together.

(Here I have highlighted that 1+3 = 4)

Patterns Within the Triangle

Diagonals

The first diagonal is, of course, just "1"s

The next diagonal has the Counting Numbers(1,2,3, etc).

The third diagonal has the triangular numbers

(The fourth diagonal, not highlighted, has the tetrahedral numbers.)

Symmetrical

The triangle is also symmetrical. The numbers on the left side have identical matching numbers on the right side, like a mirror image.

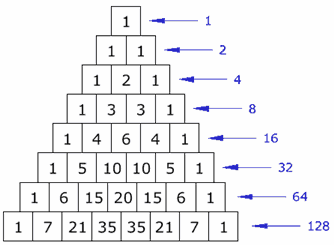
Horizontal Sums

What do you notice about the horizontal sums?

Is there a pattern?

They double each time (powers of 2).

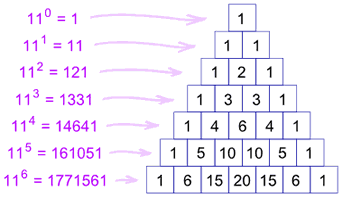
Exponents of 11

Each line is also the powers (exponents) of 11:

• 11⁰=1 (the first line is just a "1")
• 11¹=11 (the second line is "1" and "1")
• 11²=121 (the third line is "1", "2", "1")
• etc!

But what happens with 11⁵ ? Simple! The digits just overlap, like this:

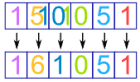
The same thing happens with 11⁶ etc.

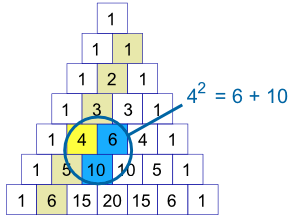
Squares

For the second diagonal, the square of a number is equal to the sum of the numbers next to it and below both of those.

Examples:

• 3² = 3 + 6 = 9,
• 4² = 6 + 10 = 16,
• 5² = 10 + 15 = 25,
• ...

There is a good reason, too ... can you think of it? (Hint: 4²=6+10, 6=3+2+1, and 10=4+3+2+1)

Fibonacci Sequence

Try this: make a pattern by going up and then along, then add up the values (as illustrated) ... you will get the Fibonacci Sequence.

(The Fibonacci Sequence starts "0, 1" and then continues by adding the two previous numbers, for example 3+5=8, then 5+8=13, etc)

Odds and Evens

If you color the Odd and Even numbers, you end up with a pattern the same as the Sierpinski Triangle

Using Pascal's Triangle

Heads and Tails

Pascal's Triangle can show you how many ways heads and tails can combine. This can then show you the probability of any combination.

For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three that will give two heads and one tail (HHT, HTH, THH), also three that give one head and two tails (HTT, THT, TTH) and one for all Tails (TTT). This is the pattern "1,3,3,1" in Pascal's Triangle.

Tosses	Possible Results (Grouped)	Pascal's Triangle
1	H T	1, 1
2	HH HT TH TT	1, 2, 1
3	HHH HHT, HTH, THH HTT, THT, TTH TTT	1, 3, 3, 1
4	HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT	1, 4, 6, 4, 1
	... etc ...

Example: What is the probability of getting exactly two heads with 4 coin tosses?

There are 1+4+6+4+1 = 16 (or 2⁴=16) possible results, and 6 of them give exactly two heads. So the probability is 6/16, or 37.5%

Combinations

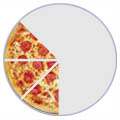
The triangle also shows you how many Combinations of objects are possible.

Example: You have 16 pool balls. How many different ways could you choose just 3 of them (ignoring the order that you select them)?

Answer: go down to the start of row 16 (the top row is 0), and then along 3 places (the first place is 0) and the value there is your answer, 560.
Here is an extract at row 16:

1    14    91    364  ...
1    15    105   455   1365  ...
1    16   120   560   1820  4368  ...

 

A Formula for Any Entry in The Triangle

In fact there is a formula from Combinations for working out the value at any place in Pascal's triangle:

It is commonly called "n choose k" and written like this: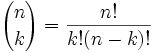

Notation: "n choose k" can also be written C(n,k), ⁿC_k or even _nC_k.

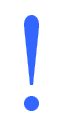The "!" is "factorial" and means to multiply a series of descending natural numbers. Examples: 4! = 4 × 3 × 2 × 1 = 24 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 1! = 1

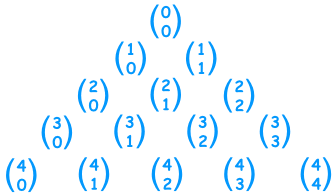
So Pascal's Triangle could also be
an "n choose k" triangle like this one.

(Note how the top row is row zero
and also the leftmost column is zero)

Example: Row 4, term 2 in Pascal's Triangle is "6" ...

... let's see if the formula works:

Yes, it works! Try another value for yourself.

This can be very useful ... you can now work out any value in Pascal's Triangle directly (without calculating the whole triangle above it).

Polynomials

Pascal's Triangle can also show you the coefficients in binomial expansion:

Power	Binomial Expansion	Pascal's Triangle
2	(x + 1)2 = 1x2 + 2x + 1	1, 2, 1
3	(x + 1)3 = 1x3 + 3x2 + 3x + 1	1, 3, 3, 1
4	(x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1	1, 4, 6, 4, 1
	... etc ...

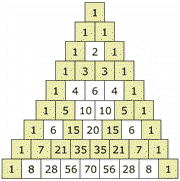
The First 15 Lines

For reference, I have included row 0 to 14 of Pascal's Triangle

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

1

5

10

10

5

1

1

6

15

20

15

6

1

1

7

21

35

35

21

7

1

1

8

28

56

70

56

28

8

1

1

9

36

84

126

126

84

36

9

1

1

10

45

120

210

252

210

120

45

10

1

1

11

55

165

330

462

462

330

165

55

11

1

1

12

66

220

495

792

924

792

495

220

66

12

1

1

13

78

286

715

1287

1716

1716

1287

715

286

78

13

1

1

14

91

364

1001

2002

3003

3432

3003

2002

1001

364

91

14

1

Week of August 18,2019

Adding and Subtracting Polynomials

A polynomial looks like this:

example of a polynomial this one has 3 terms

To add polynomials we simply add any like terms together ... so what is a like term?

Like Terms

Like Terms are terms whose variables (and their exponents such as the 2 in x²) are the same.

In other words, terms that are "like" each other.

Note: the coefficients (the numbers you multiply by, such as "5" in 5x) can be different.

Example:

7x

x

-2x

πx

are all like terms because the variables are all x

Example:

(1/3)xy2

-2xy2

6xy2

xy2/2

are all like terms because the variables are all xy²

Example: These are NOT like terms because the variables and/or their exponents are different:

2x

2x2

2y

2xy

Adding Polynomials

Two Steps:

• Place like terms together
• Add the like terms

Example: Add   2x² + 6x + 5   and   3x² - 2x - 1

Start with:2x² + 6x + 5   +   3x² − 2x − 1

Place like terms together:2x²+3x²   +   6x−2x   +   5−1

Which is:(2+3)x²  +   (6−2)x   +   (5−1)

Add the like terms:5x²  +   4x   +   4

Here is an animated example:

(Note: there was no "like term" for the -7 in the other polynomial, so we didn't have to add anything to it.)

Adding in Columns

We can also add them in columns like this:

Adding Several Polynomials

We can add several polynomials together like that.

Example: Add     (2x² + 6y + 3xy)  ,   (3x² - 5xy - x)   and   (6xy + 5)
Line them up in columns and add:

2x² + 6y + 3xy
3x²      - 5xy - x
           6xy     + 5

5x² + 6y + 4xy - x + 5

Using columns helps us to match the correct terms together in a complicated sum.

Subtracting Polynomials

To subtract Polynomials, first reverse the sign of each term we are subtracting (in other words turn "+" into "-", and "-" into "+"), then add as usual.

Like this:

Note: After subtracting 2xy from 2xy we ended up with 0, so there is no need to mention the "xy" term any more.

Source:https://www.mathsisfun.com/algebra/polynomials-adding-subtracting.html

Week of August 12, 2019

Factoring

Factors

Numbers have factors:

And expressions (like x²+4x+3) also have factors:

Factoring

Factoring (called "Factorising" in the UK) is the process of finding the factors:

Factoring: Finding what to multiply together to get an expression.

It is like "splitting" an expression into a multiplication of simpler expressions.

Example: factor 2y+6

Both 2y and 6 have a common factor of 2:

• 2y is 2 × y
• 6 is 2 × 3

So we can factor the whole expression into:

2y+6 = 2(y+3)

So 2y+6 has been "factored into" 2 and y+3

Factoring is also the opposite of Expanding:

Common Factor

In the previous example we saw that 2y and 6 had a common factor of 2

But to do the job properly we need the highest common factor, including any variables

Example: factor 3y²+12y

Firstly, 3 and 12 have a common factor of 3.
So we could have:

3y²+12y = 3(y²+4y)

But we can do better!
3y² and 12y also share the variable y.
Together that makes 3y:

• 3y² is 3y × y
• 12y is 3y × 4

So we can factor the whole expression into:

3y²+12y = 3y(y+4)

Check: 3y(y+4) = 3y × y + 3y × 4 = 3y²+12y

More Complicated Factoring

Factoring Can Be Hard !

The examples have been simple so far, but factoring can be very tricky.

Because we have to figure what got multiplied to produce the expression we are given!

It is like trying to find which ingredients
went into a cake to make it so delicious.
It can be hard to figure out!

Experience Helps

With more experience factoring becomes easier.

Example: Factor 4x² − 9

Hmmm... there don't seem to be any common factors.
But knowing the Special Binomial Products gives us a clue called the "difference of squares":

Because 4x² is (2x)², and 9 is (3)²,

So we have:

4x² − 9 = (2x)² − (3)²

And that can be produced by the difference of squares formula:

(a+b)(a−b) = a² − b²

Where a is 2x, and b is 3.

So let us try doing that:

(2x+3)(2x−3) = (2x)² − (3)² = 4x² − 9

Yes!

So the factors of 4x² − 9 are (2x+3) and (2x−3):

Answer: 4x² − 9 = (2x+3)(2x−3)

How can you learn to do that? By getting lots of practice, and knowing "Identities"!

Remember these Identities

Here is a list of common "Identities" (including the "difference of squares" used above).

It is worth remembering these, as they can make factoring easier.

a2 − b2	=	(a+b)(a−b)
a2 + 2ab + b2	=	(a+b)(a+b)
a2 − 2ab + b2	=	(a−b)(a−b)
a3 + b3	=	(a+b)(a2−ab+b2)
a3 − b3	=	(a−b)(a2+ab+b2)
a3+3a2b+3ab2+b3	=	(a+b)3
a3−3a2b+3ab2−b3	=	(a−b)3

There are many more like those, but those are the most useful ones.

Advice

The factored form is usually best.

When trying to factor, follow these steps:

"Factor out" any common terms
See if it fits any of the identities, plus any more you may know
Keep going till you can't factor any more

There are also Computer Algebra Systems (called "CAS") such as Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce and many more that are good at factoring.

More Examples

Experience does help, so here are more examples to help you on the way:

Example: w⁴ − 16

An exponent of 4? Maybe we could try an exponent of 2:

w⁴ − 16 = (w²)² − 4²

Yes, it is the difference of squares

w⁴ − 16 = (w² + 4)(w² − 4)

And "(w² − 4)" is another difference of squares

w⁴ − 16 = (w² + 4)(w + 2)(w − 2)

That is as far as I can go (unless I use imaginary numbers)

Example: 3u⁴ − 24uv³

Remove common factor "3u":

3u⁴ − 24uv³ = 3u(u³ − 8v³)

Then a difference of cubes:

3u⁴ − 24uv³ = 3u(u³ − (2v)³)

= 3u(u−2v)(u²+2uv+4v²)

That is as far as I can go.

Example: z³ − z² − 9z + 9

Try factoring the first two and second two separately:

z²(z−1) − 9(z−1)

Wow, (z-1) is on both, so let us use that:

(z²−9)(z−1)

And z²−9 is a difference of squares

(z−3)(z+3)(z−1)

source: https://www.mathsisfun.com/algebra/factoring.html

Week of August 5, 2019

Algebra 2

Complex Number

Complex Numbers

 
A Complex Number

A Complex Number is a combination of a
Real Number and an Imaginary Number

Real Numbers are numbers like:

1

12.38

−0.8625

3/4

√2

1998

Nearly any number you can think of is a Real Number!

Imaginary Numbers when squared give a negative result.

Normally this doesn't happen, because:

• when we square a positive number we get a positive result, and
• when we square a negative number we also get a positive result (because a negative times a negative gives a positive), for example −2 × −2 = +4

But just imagine such numbers exist, because we will need them.

The "unit" imaginary number (like 1 for Real Numbers) is i, which is the square root of −1

Because when we square i we get −1

i² = −1

Examples of Imaginary Numbers:

3i

1.04i

−2.8i

3i/4

(√2)i

1998i

And we keep that little "i" there to remind us we need to multiply by √−1

Complex Numbers

A Complex Number is a combination of a Real Number and an Imaginary Number:

Examples:

1 + i

39 + 3i

0.8 − 2.2i

−2 + πi

√2 + i/2

Can a Number be a Combination of Two Numbers?

Can we make up a number from two other numbers? Sure we can!

We do it with fractions all the time. The fraction ³/₈ is a number made up of a 3 and an 8. We know it means "3 of 8 equal parts".

Well, a Complex Number is just two numbers added together (a Real and an Imaginary Number).

Either Part Can Be Zero

So, a Complex Number has a real part and an imaginary part.

But either part can be 0, so all Real Numbers and Imaginary Numbers are also Complex Numbers.

Complex Number	Real Part	Imaginary Part
3 + 2i	3	2
5	5	0	Purely Real
−6i	0	−6	Purely Imaginary

Complicated?

Complex does not mean complicated.

It means the two types of numbers, real and imaginary, together form a complex, just like a building complex (buildings joined together).

A Visual Explanation

You know how the number line goes left-right?

Well let's have the imaginary numbers go up-down:

And we get the Complex Plane

A complex number can now be shown as a point:

The complex number 3 + 4i

Adding

To add two complex numbers we add each part separately:

(a+bi) + (c+di) = (a+c) + (b+d)i

Example: add the complex numbers 3 + 2i and 1 + 7i

• add the real numbers, and
• add the imaginary numbers:

(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7)i
= 4 + 9i

Let's try another:

Example: add the complex numbers 3 + 5i and 4 − 3i

(3 + 5i) + (4 − 3i)
= 3 + 4 + (5 − 3)i
= 7 + 2i

On the complex plane it is:

Multiplying

To multiply complex numbers:

Each part of the first complex number gets multiplied by
each part of the second complex number

Just use "FOIL", which stands for "Firsts, Outers, Inners, Lasts" (see Binomial Multiplication for more details):

	Firsts: a × c Outers: a × di Inners: bi × c Lasts: bi × di
(a+bi)(c+di) = ac + adi + bci + bdi2

Like this:

Example: (3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i)= 3×1 + 3×7i + 2i×1+ 2i×7i

 = 3 + 21i + 2i + 14i²

 = 3 + 21i + 2i − 14  (because i² = −1)

 = −11 + 23i

And this:

Example: (1 + i)²

(1 + i)(1 + i)= 1×1 + 1×i + 1×i + i²

 = 1 + 2i − 1  (because i² = −1)

 = 0 + 2i

But There is a Quicker Way!

Use this rule:

(a+bi)(c+di) = (ac−bd) + (ad+bc)i

Example: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i

Why Does That Rule Work?

It is just the "FOIL" method after a little work:

(a+bi)(c+di) =ac + adi + bci + bdi²  FOIL method

 =ac + adi + bci − bd  (because i² = −1)

 =(ac − bd) + (ad + bc)i  (gathering like terms)

And there we have the (ac − bd) + (ad + bc)i  pattern.

This rule is certainly faster, but if you forget it, just remember the FOIL method.

Let us try i²

Just for fun, let's use the method to calculate i²

Example: i²

We can write i with a real and imaginary part as 0 + i

i² = (0 + i)²= (0 + i)(0 + i)

 = (0×0 − 1×1) + (0×1 + 1×0)i

 = −1 + 0i

 = −1

And that agrees nicely with the definition that i² = −1

So it all works wonderfully!

Learn more at Complex Number Multiplication.

Conjugates

We will need to know about conjugates in a minute!

A conjugate is where we change the sign in the middle like this:

A conjugate is often written with a bar over it:

Example:

5 − 3i   =   5 + 3i

Dividing

The conjugate is used to help complex division.

The trick is to multiply both top and bottom by the conjugate of the bottom.

Example: Do this Division:

2 + 3i4 − 5i

Multiply top and bottom by the conjugate of 4 − 5i :

2 + 3i4 − 5i×4 + 5i4 + 5i  =  8 + 10i + 12i + 15i²16 + 20i − 20i − 25i²

Now remember that i² = −1, so:

=  8 + 10i + 12i − 1516 + 20i − 20i + 25

Add Like Terms (and notice how on the bottom 20i − 20i cancels out!):

=  −7 + 22i41

Lastly we should put the answer back into a + bi form:

=  −7 41 + 2241i

DONE!

Yes, there is a bit of calculation to do. But it can be done.

Multiplying By the Conjugate

There is a faster way though.

In the previous example, what happened on the bottom was interesting:

(4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i²

The middle terms (20i − 20i) cancel out! Also i² = −1 so we end up with this:

(4 − 5i)(4 + 5i) = 4² + 5²

Which is really quite a simple result. The general rule is:

(a + bi)(a − bi) = a² + b²

We can use that to save us time when do division, like this:

Example: Let's try this again

2 + 3i4 − 5i

Multiply top and bottom by the conjugate of 4 − 5i :

2 + 3i4 − 5i×4 + 5i4 + 5i  =  8 + 10i + 12i + 15i²16 + 25

=  −7 + 22i41

And then back into a + bi form:

=  −7 41 + 2241i

DONE!

Notation

We often use z for a complex number. And Re() for the real part and Im() for the imaginary part, like this:

Which looks like this on the complex plane:

The Mandelbrot Set

	The beautiful Mandelbrot Set (pictured here) is based on Complex Numbers. It is a plot of what happens when we take the simple equation z2+c (both complex numbers) and feed the result back into z time and time again. The color shows how fast z2+c grows, and black means it stays within a certain range.
Here is an image made by zooming into the Mandelbrot set
And here is the center of the previous one zoomed in even further:	Reference:https://www.mathsisfun.com/numbers/complex-numbers.html