Week of March 26, 2018

Algebra 1

Characteristics of Graphs of Exponential Functions

LEARNING OBJECTIVES

• Determine whether an exponential function and it’s associated graph represents growth or decay
• Sketch a graph of an exponential function

Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form $f\left(x\right)=b^x$ whose base is greater than one. We’ll use the function $f\left(x\right)=2^x$. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
$f\left(x\right)=2^x$	$\frac{1}{8}$	$\frac{1}{4}$	$\frac{1}{2}$	1	2	4	8

Each output value is the product of the previous output and the base, 2. We call the base 2 the constant ratio. In fact, for any exponential function with the form $f\left(x\right)=a{b}^x$, b is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of a.

Notice from the table that

• the output values are positive for all values of x;
• as x increases, the output values increase without bound; and
• as x decreases, the output values grow smaller, approaching zero.

The graph below shows the exponential growth function $f\left(x\right)=2^x$.

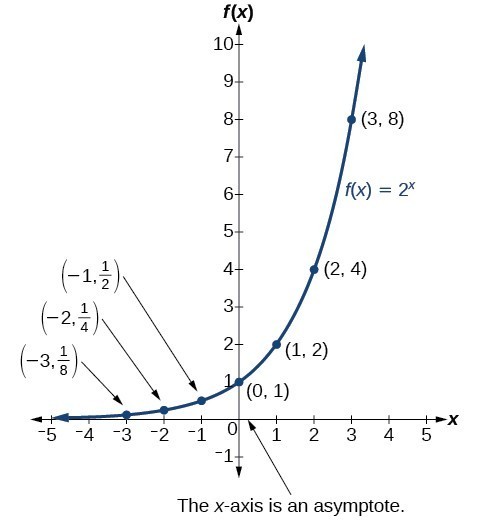
Notice that the graph gets close to the x-axis, but never touches it.

The domain of $f\left(x\right)=2^x$ is all real numbers, the range is $\left(0,\infty \right)$, and the horizontal asymptote is $y=0$.

To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form $f\left(x\right)=b^x$ whose base is between zero and one. We’ll use the function $g\left(x\right)={\left(\frac{1}{2}\right)}^x$. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
$g\left(x\right)={\left(\frac{1}{2}\right)}^x$	8	4	2	1	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$

Again, because the input is increasing by 1, each output value is the product of the previous output and the base, or constant ratio $\frac{1}{2}$.

Notice from the table that

• the output values are positive for all values of x;
• as x increases, the output values grow smaller, approaching zero; and
• as x decreases, the output values grow without bound.

The graph shows the exponential decay function, $g\left(x\right)={\left(\frac{1}{2}\right)}^x$.

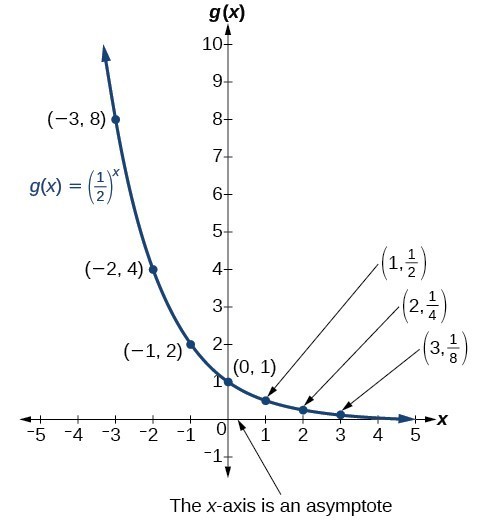
The domain of $g\left(x\right)={\left(\frac{1}{2}\right)}^x$ is all real numbers, the range is $\left(0,\infty \right)$, and the horizontal asymptote is $y=0$.

A GENERAL NOTE: CHARACTERISTICS OF THE GRAPH OF THE PARENT FUNCTION F(X) = B^X

An exponential function with the form $f\left(x\right)=b^x$, $b>0$, $b\ne 1$, has these characteristics:

• one-to-one function
• horizontal asymptote: $y=0$
• domain: $\left(-\infty ,\infty \right)$
• range: $\left(0,\infty \right)$
• x-intercept: none
• y-intercept: $\left(0,1\right)$
• increasing if $b>1$
• decreasing if $b<1$
• $\mathrm{<br>}$

https://courses.lumenlearning.com/waymakercollegealgebra/chapter/characteristics-of-graphs-of-exponential-functions/

Algebra 2

Adding fractions with equal denominators

Factions that have equal denominators are also called like fractions.

To add or subtract two like fractions, simply add or subtract the numerators and put the result over the common denominator, like this:

Example:   

---

Adding fractions with unequal denominators

To add or subtract fractions don’t have equal denominators, they must first be converted to equivalent fractions that do have a common denominator. Here are the steps: Find the least common multiple of the denominators. When applied to fractions this number is called the least common denominator (LCD) of the fractions. Convert each fraction to an equivalent fraction that has the LCD as its denominator. To do this, multiply the numerator and denominator of each fraction by the appropriate factor that makes this happen. Add the numerators and place over the common denominator. Simplify the result by reducing it to lowest terms.

Example: .     To subtract these fractions, the steps are:

1. Find the LCD, which is 10.
2. Since the first fraction already has the LCD as its denominator, we need only multiply the second fraction by 5/5 to convert it to an equivalent fraction with a denominator of 10.
3. Subtract the numerators and place the result over the LCD.
4. Simplify by reducing the fraction to lowest terms.

   

---

Example: .     To add these fractions, the steps are:

1. Find the LCD, which is (4 x − 1)(x + 3).
   
2. Multiply the numerator and denominator of the first fraction by (x + 3) and the numerator and denominator of the second fraction by (4 x − 1):

   

3. The two fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.

   

4. Simplify by distributing the numerator.

   

---

Adding fractions with factorable denominators

You must always factor the denominators. This is the only way to tell if a factor appears in more than one denominator.

Example: .     To add these fractions, the steps are:

1. Factor the denominator of the first fraction. Then we can see that the factors x − 2 and x − 3 appear in more than one denominator:

   

2. Find the LCD, which is (x − 2)(x − 3).
   
3. Multiply the numerator and denominator of the second fraction by (x − 3) and the numerator and denominator of the third fraction by (x − 2):

   

4. The three fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.

   

5. Simplify by distributing and adding like terms in the numerator.

   

---

Adding fractions and non-fractions (mixed expressions)

To add or subtract fractions and non-fractions, convert the non-fractions into fractions with denominators of 1.

Example: .     To add this fraction and non-fraction, the steps are:

1. Write the non-fraction as a fraction with a denominator of 1:

   

2. Find the LCD, which of course, is (x − 2).
   
3. Multiply the numerator and denominator of the first fraction by (x − 2):

   

4. The two fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.

   

5. Simplify by distributing and adding like terms in the numerator.

   

http://mathonweb.com/help_ebook/html/frac_expr_3.htm