Week of March 5, 2018

Algebra 1

Completing the Square

"Completing the Square" is where we ... 

... take a Quadratic Equation like this:		and turn it into this:
ax2 + bx + c = 0		a(x+d)2 + e = 0

For those of you in a hurry, I can tell you that:d = b2a

and:e = c − b²4a

But if you have time, let me show you how to "Complete the Square" yourself.

Completing the Square

Say we have a simple expression like x² + bx. Having x twice in the same expression can make life hard. What can we do?

Well, with a little inspiration from Geometry we can convert it, like this:

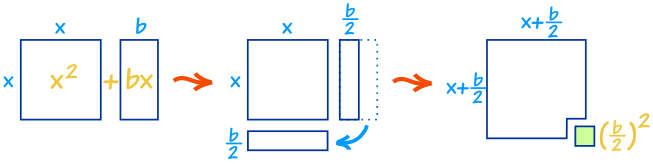
As you can see x² + bx can be rearranged nearly into a square ...

... and we can complete the square with (b/2)²

In Algebra it looks like this:

x2 + bx	+ (b/2)2	=	(x+b/2)2
	"Complete the Square"

So, by adding (b/2)² we can complete the square.

And (x+b/2)² has x only once, which is easier to use.

Keeping the Balance

Now ... we can't just add (b/2)² without also subtracting it too! Otherwise the whole value changes.

So let's see how to do it properly with an example:

Start with:
	("b" is 6 in this case)
Complete the Square:
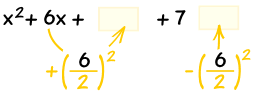
	Also subtract the new term
Simplify it and we are done.

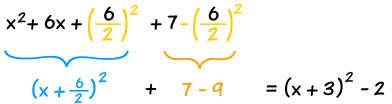The result:

x² + 6x + 7   =   (x+3)² − 2

And now x only appears once, and our job is done!

A Shortcut Approach

Here is a quick way to get an answer you may like.

First think about the result we want: (x+d)² + e

After expanding (x+d)² that becomes: x² + 2dx + d² + e

Now see if we can turn our example into x² + 2dx + d² + e form to discover d and e

Example: try to fit x² + 6x + 7 into x² + 2dx + d² + e

Now we can "force" an answer:

• We know that 6x must end up as 2dx, so d must be 3
• Next we see that 7 must become d² + e = 9 + e, so e must be −2

And we get the same result (x+3)² − 2 as above!

https://www.mathsisfun.com/algebra/completing-square.html


Algebra 2

Factoring and Graphing PolynomialsMathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

The skill of factoring is a helpful tool when graphing polynomial functions.
(In Algebra 1, PARCC is limiting this task to quadratic and cubic polynomial functions with linear and quadratic factors.)

A polynomial function is a function which is defined by a polynomial. (In plain English, it's a polynomial expression set equal to f(x), or some other notation.) Examples:   f(x) = x2 + x - 6;      P(x) = x3 - x2 - 12x;      y1 = x2 + 4x + 4

Basic information about the graphs of polynomial functions:

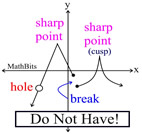
1. Continuous: The graphs of polynomial functions are continuous. You can draw the entire function without lifting your pencil from your paper.

2. Smooth: The graphs of polynomial functions are always nice smooth graphs.  The graphs do not contain holes, breaks or sharp point corners.

3. Turning Points: The "hills" or "valleys" where the graph changes direction from increasing to decreasing, or from decreasing to increasing, are often called turning points.  The number of turning points is never more than the degree of the polynomial minus one. For example, the graph of a 3rd degree polynomial function can have 2 turning points or fewer. [If the degree is n, the number of turning points is at most n - 1. There could be fewer.] Other terms for turning points can be relative maximum (or minimum) and local maximum(or minimum). The designation of "relative" (or "local") tells you that while this point may be a turning point, it may not be the maximum (or mininum) value reached by this function. It is only a maximim (or minimum) "relative" to a small section of the function surrounding this point. The one, true, largest (or smallest) value reached by the entire function is called the absolute maximum (or minimum), or the global maximum (or minimum). FYI: The plural of maximum is maxima. The plural of minimum is minima. Discussions of maxima and minima are referred to as extrema.

Here's where the factoring connection comes in to play:

4. Roots (or Zeros): If you plug in r (some real number) for x in a polynomial function, P(x), and get an answer of 0, the number, r, is called a root, or zero, of the polynomial. It can be quite tedious to repeatedly test random numbers looking for those numbers that give an answer of zero. A faster method for finding these roots (or zeros), is to factor the polynomial, and then set the factors equal to zero (the desired answer). This factoring method for finding roots, or zeros, utilizes thezero factor principle which states that "if a • b = 0, then either a = 0 and/or b = 0."  The real numbers that create the roots (or zeros) of a polynomial correspond to the x-intercepts of the graph of the polynomial function. This is valuable information when it comes to creating the graph of a polynomial (without a graphing calculator). It is also valuable if you are given the graph and are attempting to create a possible equation.  Note: A polynomial of degree 2 will have two roots (zeros), a polynomial of degree 3 will have three roots (zeros), and so on.

Example:

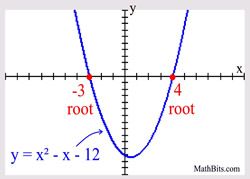What happens when a factor repeats?

5. Multiplicity of Roots (or Zeros): We have seen in section 4 that the roots (zeros) of a polynomial correspond with the x-intercepts of the polynomial graph. In some situations, the graph will "cross" the x-axis at these points. In other situations, the graph may simply "touch" (be tangent to) the x-axis at these points. Let's see if we can determine, before we draw the graph, whether it will "cross" the x-axis at each root, or simply "touch" (be tangent to) the x-axis at each root. 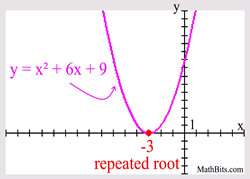Consider the example at the right. The polynomial is of degree two, so there will be two roots (zeroes). The factor of (x + 3) is repeated twice, and can also be written as (x + 3)2. The number of times a factor appears in a polynomial is referred to as its multiplicity. In the example at the right, the factor (x + 3) has a multiplicity of 2, since it appears twice. It creates a "repeated root".  Multiplicity EVEN: When the multiplicity (the number of times a factor repeats) is two (or even), the graph will just "touch" (be tangent to) the x-axis at that point. Why? "EVEN" multiplicities are factors that occur an even number of times, and form squares. Since squares are always positive, the graph near the root (zero) will not change signs from positive (above the x-axis) to negative (below the x-axis), or vice versa. The graph will "touch" the x-axis at the root (zero) but remain on the same side of the x-axis.

Example degree 2:

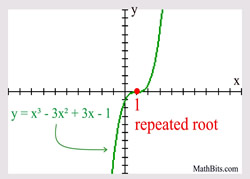
What if the multiplicity is ODD? Consider the example at the right. The polynomial is of degree three, so there will be three roots (zeros). The factor of (x - 1) appears three times, and can be written as (x - 1)3.  Multiplicity ODD: When the multiplicity (the number of times a factor repeats) is three (or odd), the graph will "cross" the x-axis at that point. Did you notice?  If you see a factor such as (x - 1)3, the multiplicity is 3. If you see a factor such as (x + 2)2, the multiplicity is 2. If you see a factor such as (x + 3), the multiplicity is 1.  Note: When you factor a polynomial, the sum of the multiplicities equals the degree of the polynomial. x3 + x2 - 5x + 3 = (x - 1)2(x + 3) = (x - 1)2(x + 3)1 degree = 3 sum of multiplicities = 2 + 1 = 3

Example degree 3:

There is one more thing we can find out before we graph!

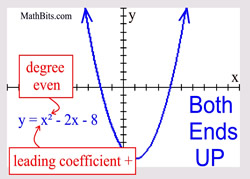
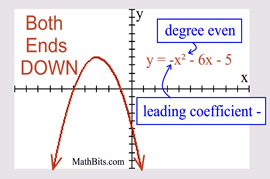
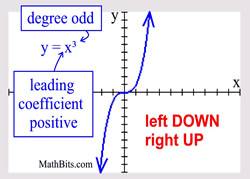
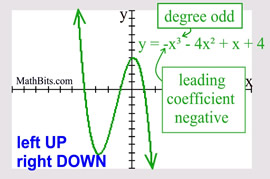
6. End Behavior: Looking at a few aspects of a polynomial will tell us what is happening at either end of the graph. We will be looking at the DEGREE of the polynomial and the SIGN of the leading coefficient to determine what is happening to the graph. End behavior refers to the appearance of a graph as it is followed indefinitely in either direction.
Even Degree Polynomial ("ends" behave similar to a quadratic) Leading coefficient POSITIVE: both "ends" are UP. Leading coefficient NEGATIVE: both "ends" are DOWN.	Odd Degree Polynomial ("ends" behave similar to a cubic) Leading coefficient POSITIVE: left end is DOWN and right end is UP. Leading coefficient NEGATIVE: left end is UP and right end is DOWN. https://mathbitsnotebook.com/Algebra1/Factoring/FCGraphing.html