Week of April 30,2018

Algebra 1

The slope-intercept form of a linear equation

Earlier in this chapter we have expressed linear equations using the standard form Ax + By = C. Now we're going to show another way of expressing linear equations by using the slope-intercept form y = mx + b.

In the slope-intercept form you use the slope of the line and the y-intercept to express the linear function.

y=mx+b$$y=mx+b$$

Where m is the slope and b is the y-intercept.

---

Example

Graph the equation

y−2x=1$$y-2x=1$$

rewrite in slope-intercept form

y=2x+1$$y=2x+1$$

Identify the slope and the y-intercept

m = 2 and b = 1

Plot the point corresponding to the y-intercept, (0,1)

The m-value, the slope, tells us that for each step to the right on the x-axis we move 2 steps upwards on the y-axis (since m = 2)

And once you have your second point you can just draw a line through the two points and extend it in both directions.

You can check to see that the line you've drawn is the correct one by substituting the coordinates of the second point into the original equation. If the equation holds true than the second point is correct.

Our second point = (1, 3)

y−2x=1$$y-2x=1$$

3−2⋅1=3−2=1$$3-2\cdot 1=3-2=1$$

Our second point is a solution to the equation i.e. the line we drew is correct.

A line that passes through the origin has a y-intersect of zero, b = 0, and represents a direct variation.

y=mx$$y=mx$$

In a direct variation the nonzero number m is called the constant of variation.

You can name a function, f by using the function notion

f(x)=mx+b$$f\left(x\right)=mx+b$$

f(x) is another name for y and is read as "the value of f at x" or "f of x". You can use other letters than f to name functions.

A group of functions that have similar characteristics are called a family of functions. All functions that can be written on the form f(x) = mx + b belong to the family of linear functions.

The most basic function in a family of functions is called the parent function. The parent function of all linear functions is

f(x)=x$$f\left(x\right)=x$$

---

Video lesson

Graph y = 3x - 2

https://www.mathplanet.com/education/algebra-1/visualizing-linear-functions/the-slope-intercept-form-of-a-linear-equation

Algebra 2

Solving Log Equations

There are two basic forms for solving logarithmic equations:

               

               

Not every equation will start out in these forms, but you'll be able to use the tricks from the last section to get them there.

With these forms, we'll just need one big thing to finish them off:

THE POWER OF INVERSES!

Let's review for a minute:

What do inverse functions do to each other?

If you don't know that off the top of your head, go back and review that stuff or you're going to be one miserable puppy!

OK, what do inverse functions do to each other?

They undo each other!

Remember that

and

are inverses...

So,

undoes

!

Remember that

and

(really

)

are inverses...  So,

undoes

!

Remember that

and

(really

)

are inverses...  So,

undoes

!

Also remember that, whatever you do to one side of an equation, you have to do to the other.

http://www.coolmath.com/algebra/17-exponentials-logarithms/15-solving-logarithmic-equations-01

Week of April 23, 2018

ALGEBRA 1

Compare Linear, Exponential, and Quadratic Models

Linear Has an x with no exponent.

Exponential Has an x as the exponent.

Quadratic Has an x2 in the equation; the highest power is 2.

Identifying from a graph:

 Linear Makes a straight line

 Quadratic Makes a U or ∩ (parabola)

Exponential Rises or falls quickly in one direction



ALGEBRA 2

Solving Exponential Equations

To solve exponential equations without logarithms, you need to have equations with comparable exponential expressions on either side of the "equals" sign, so you can compare the powers and solve. In other words, you have to have "(some base) to (some power) equals (the same base) to (some other power)", where you set the two powers equal to each other, and solve the resulting equation. For example:

• Solve 5x = 53

Since the bases ("5" in each case) are the same, then the only way the two expressions could be equal is for the powers also to be the same. That is:

x = 3

This solution demonstrates the logical basis for how this entire class of equation is solved: If the bases are the same, then the powers must also be equal; this is the only way for the two sides of the equation to be equal to each other. Since the powers must be the same, then we can set the two powers equal to each other, and solve the resulting equation.

---

• Solve $\mathbf{\color{green}{ 10^{1-\mathit{x}} = 10^4 }}$

Since the bases are the same, then I can equate the powers and solve:

1 – x = 4

1 – 4 = x

–3 = x

Then my solution is:

x = –3

---

Not all exponential equations are given in terms of the same base on either side of the "equals" sign. Sometimes we first need to convert one side or the other (or both) to some other base before we can set the powers equal to each other. For example:

• Solve 3x = 9

Since 9 = 32, this is really asking me to solve:

3x = 32

By converting the 9 to a 32, I've converted the right-hand side of the equation to having the same base as the left-hand side. Since the bases are now the same, I can set the two powers equal to each other:

x = 2

---

• Solve $\mathbf{\color{green}{ 3^{2\mathit{x}-1} = 27 }}$

In this case, I have an exponential on one side of the "equals" and a number on the other. I can solve the equation if I can express the "27" as a power of 3. Since 27 = 33, then I can convert and proceed with the solution:

32x–1 = 27

32x–1 = 33

2x – 1 = 3

2x = 4

x = 2

If I'm not sure of my answer, or if I want to check it before I hand it in (on, say, a test), I can check it by plugging it back into the original exercise. The power on the left-hand side of the original equation would simplify as:

2x – 1 = 2(2) – 1

= 4 – 1 = 3

And 33 = 27, which is the right-hand side of the original equation. Then my (confirmed) solution is:

x = 2

http://www.purplemath.com/modules/solvexpo.htm

Week of April 16, 2018

Algebra 1

Correlation

When the two sets of data are strongly linked together we say they have a High Correlation.

The word Correlation is made of Co- (meaning "together"), and Relation

• Correlation is Positive when the values increase together, and
• Correlation is Negative when one value decreases as the other increases

Like this:

(Learn More About Correlation)

Negative Correlation

Correlations can be negative, which means there is a correlation but one value goes down as the other value increases.

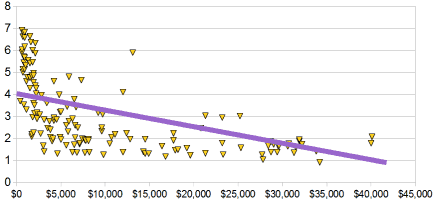
Example : Birth Rate vs Income The birth rate tends to be lower in richer countries. Below is a scatter plot for about 100 different countries.

Country Yearly Production per Person Birth Rate Madagascar $800 5.70 India $3,100 2.85 Mexico $9,600 2.49 Taiwan $25,300 1.57 Norway $40,000 1.78

It has a negative correlation (the line slopes down)

https://www.mathsisfun.com/data/scatter-xy-plots.html

ALGEBRA 2

Rationals

Home > Breadcrumbs > Rationals

Rationals: Basics :: Simplifying :: Graphing :: Practice Problems :: Quiz

BASICS: (top)

A rational function is a function of the form  where  and p(x) and q(x) are polynomials.

SIMPLIFYING: (top)

-> see also: Factoring & Expanding

Simplifying rational expressions is fundamental to graphing rational functions and solving rational equations. To simplify a rational expression, follow these steps:

1. Factor the polynomials in both the numerator and denominator
2. Cancel out like terms
3. Keep track of restrictions on domain

This last step is extremely important. If a certain value of x makes the denominator of the rational 0 at any point, the rational is undefined at that point and it is not part of the domain. Let's consider an example.

EXAMPLE 1:Problem: Simplify the rational function .
Solution: First, factor the numerator and denominator to get . Then, cancel out the common term (x+2) to get the simplified function . This is not the full answer, however; the domain of this function is restricted. If one plugs either the point x=2 or x=-2 to this simplified function, one finds f(0)=0. This is not correct, though, as if either x=2 or x=-2 is plugged into the original function one finds , which is undefined. Thus, one simplifying, one must include the domain restrictions. The final answer, then, is .
EXAMPLE 2:Problem: Simplify the rational function .
Solution: First, rewrite the division as multiplication and factor everything: . Then, cancel out identical terms, keeping track of the restrictions from the denominator (x≠5, -2, -3) to get .

GRAPHING: (top)

-> see also: Manipulating Graphs

Graphing rationals has much in common with graphing polynomials. As with polynomials, we wish to show end behavior, the y-intercept, x-intercepts, and behavior at roots. The y-intercept, x-intercepts, and behavior at roots are found the same way for rational functions as for polynomials. There are differences in end behavior, and we are also concerned with asymptotes, which are not found in graphs of polynomials.

End Behavior

The end behavior of rational functions is more complicated than that of polynomials and is easiest to study if broken down into cases.

Case 1: Degree in Denominator is Greater than Degree in Numerator

In this case, where the degree of the denominator is greater than the degree in the numerator, . As , the polynomial in the denominator grows much faster than the polynomial in the numerator, so their quotient approaches to 0.

The image below shows a graph of  showing this end behavior.

Case 2: Same Degree in Numerator and Denominator

As , only the first term (term with the greatest degree) in each polynomial becomes significant. That is, for a rational function such as , we can determine the end behavior by looking at the function . Since ,  and . This results in a horizontal asymptote at y=1 that the graph approaches but never reaches as .

To sum up, the end behavior of a rational function with the same degree in the numerator and denominator is determined by the quotient of the leading coefficients of the two polynomials.

EXAMPLE 3:Problem: State the end behavior of the rational .
Solution: First, for visual clarity, rearrange the terms so that the leading term of each polynomial is written first: . As , only the first term in each polynomial becomes significant, so we can look at the behavior of . The x³ terms cancel out, leaving . Thus, . The image below is a graph of  exhibiting this end behavior.
Note that the graph can cross the asymptote, which it does in this example. It then approaches the asymptote from the opposite side as .

Case 3: Degree in Numerator is Greater than Degree In Denominator

There is one special case when the degree in the numerator of a rational is greater than the degree in the denominator that deserves our immediate attention. In this special case, the degree of the numerator is only greater than the degree of the denominator by one and a common factor cancels out, such has in the rational . Here, the (x-3) term cancels out, giving . Thus, the graph is identical to that of the linear function , except that the graph of f(x) has a point discontinuity at x=3. In this special case, then, the end behavior of the function is identical to that of a linear function; namely,  and . This is shown in the graph of  below.

In most situations where the degree in the numerator is greater than the degree in the denominator, there are not terms that can be cancelled out. To graph these rationals, one must determine their end behavior using polynomial long division or synthetic division. This division will result in an expression of the form where R(x) is the remainder after the division (and Q(x) is the polynomial in the denominator). Because the degree of Q(x) is greater than the degree of R(x), . Since  and , . This resulting linear function y=ax+b is called an oblique asymptote. Note that the limit of oblique asymptote, and thus of the original rational, is  and  if a>0 and the opposite if a<0, so it is correct to say that  and  (for a >0; or the opposite for a<0). It is more specific and useful, particularly for graphing, however, to find the oblique asymptote. This procedure will become more clear with an example.

EXAMPLE 4:Problem: Find the oblique asymptote of the rational .
Solution: First note that there are no common factors in the numerator and denominator that can be cancelled out. Next, use long division or synthetic division to find . Thus, there is an oblique asymptote at y=x+2. This is shown in the graph below.

Vertical Asymptotes

You probably noticed a number of vertical lines in the graphs of rationals in the preceding examples. These are vertical asymptotes, which result when the denominator of a rational that has no common factors to cancel in its numerator and denominator is equal to zero. The function is undefined at this point.

How do graphs behave around vertical asymptotes? There are two possibilities. As x approaches the asymptote, the graph approaches either positive or negative infinity, as shown in the image at right. The notation  and  are used to denote the behavior of a graph as it approaches an asymptote at x=C from the left and right respectively. Thus, for the graph at right,  and .

Or course, we wish to be able to predict how a graph will behave around a particular vertical asymptote. As with roots, the behavior around the asymptote is determined by its multiplicity. If the multiplicity of the asymptote is odd, the behavior across the asymptote is opposite; if the graph approaches positive infinity from one side, it must approach negative infinity from the other. If the multiplicity of the asymptote is even, however, the graph has the same limit regardless of which time direction it approaches the asymptote. These two possibilities are shown below.

Note that you only know that the behavior will be the same or opposite; additional information, such as the y-intercept and roots, must be used to determine where the graph goes up and down.

---

Determining the end behavior, y-intercept, x-intercepts, behavior at roots, and vertical asymptotes of a rational function can yield a useful graph of the function. Putting all of this information together to develop a coherent picture of what's going on can take some time; the best way to get better at it is to practice with problems.

https://www.math.brown.edu/utra/rationals.html