Week of October 29, 2018

Astronomy

The Life Cycles of Stars: How Supernovae Are Formed

It is very poetic to say that we are made from the dust of the stars. Amazingly, it's also true! Much of our bodies, and our planet, are made of elements that were created in the explosions of massive stars. Let's examine exactly how this can be.

Life Cycles of Stars

A star's life cycle is determined by its mass. The larger its mass, the shorter its life cycle. A star's mass is determined by the amount of matter that is available in its nebula, the giant cloud of gas and dust from which it was born. Over time, the hydrogen gas in the nebula is pulled together by gravity and it begins to spin. As the gas spins faster, it heats up and becomes as a protostar. Eventually the temperature reaches 15,000,000 degrees and nuclear fusion occurs in the cloud's core. The cloud begins to glow brightly, contracts a little, and becomes stable. It is now a main sequence star and will remain in this stage, shining for millions to billions of years to come. This is the stage our Sun is at right now.

As the main sequence star glows, hydrogen in its core is converted into helium by nuclear fusion. When the hydrogen supply in the core begins to run out, and the star is no longer generating heat by nuclear fusion, the core becomes unstable and contracts. The outer shell of the star, which is still mostly hydrogen, starts to expand. As it expands, it cools and glows red. The star has now reached the red giant phase. It is red because it is cooler than it was in the main sequence star stage and it is a giant because the outer shell has expanded outward. In the core of the red giant, helium fuses into carbon. All stars evolve the same way up to the red giant phase. The amount of mass a star has determines which of the following life cycle paths it will take from there.

The life cycle of a low mass star (left oval) and a high mass star (right oval).

The illustration above compares the different evolutionary paths low-mass stars (like our Sun) and high-mass stars take after the red giant phase. For low-mass stars (left hand side), after the helium has fused into carbon, the core collapses again. As the core collapses, the outer layers of the star are expelled. A planetary nebula is formed by the outer layers. The core remains as awhite dwarf and eventually cools to become a black dwarf.

On the right of the illustration is the life cycle of a massive star (10 times or more the size of our Sun). Like low-mass stars, high-mass stars are born in nebulae and evolve and live in the Main Sequence. However, their life cycles start to differ after the red giant phase. A massive star will undergo a supernova explosion. If the remnant of the explosion is 1.4 to about 3 times as massive as our Sun, it will become a neutron star. The core of a massive star that has more than roughly 3 times the mass of our Sun after the explosion will do something quite different. The force of gravity overcomes the nuclear forces which keep protons and neutrons from combining. The core is thus swallowed by its own gravity. It has now become a black hole which readily attracts any matter and energy that comes near it. What happens between the red giant phase and the supernova explosion is described below.

From Red Giant to Supernova: The Evolutionary Path of High Mass Stars

Once stars that are 5 times or more massive than our Sun reach the red giant phase, their core temperature increases as carbon atoms are formed from the fusion of helium atoms. Gravity continues to pull carbon atoms together as the temperature increases and additional fusion processes proceed, forming oxygen, nitrogen, and eventually iron.

The two supernovae, one reddish yellow and one blue, form a close pair just below the image center (to the right of the galaxy nucleus) Image Credit: C. Hergenrother, Whipple Observatory, P. Garnavich, P.Berlind, R.Kirshner (CFA).

When the core contains essentially just iron, fusion in the core ceases. This is because iron is the most compact and stable of all the elements. It takes more energy to break up the iron nucleus than that of any other element. Creating heavier elements through fusing of iron thus requires an input of energy rather than the release of energy. Since energy is no longer being radiated from the core, in less than a second, the star begins the final phase of gravitational collapse. The core temperature rises to over 100 billion degrees as the iron atoms are crushed together. The repulsive force between the nuclei overcomes the force of gravity, and the core recoils out from the heart of the star in a shock wave, which we see as a supernova explosion.

As the shock encounters material in the star's outer layers, the material is heated, fusing to form new elements and radioactive isotopes. While many of the more common elements are made through nuclear fusion in the cores of stars, it takes the unstable conditions of the supernova explosion to form many of the heavier elements. The shock wave propels this material out into space. The material that is exploded away from the star is now known as a supernova remnant.

The hot material, the radioactive isotopes, as well as the leftover core of the exploded star, produce X-rays and gamma-rays.

For the Student Using the above background information, (and additional sources of information from the library or the web), make your own diagram of the life cycle of a high-mass star.

For the Student Using the text, and any external printed references, define the following terms: protostar, life cycle, main sequence star, red giant, white dwarf, black dwarf, supernova, neutron star, pulsar, black hole, fusion, element, isotope, X-ray, gamma-ray.

---

Reference URLs:

Supernovae
http://imagine.gsfc.nasa.gov/science/objects/supernovae1.html
http://imagine.gsfc.nasa.gov/science/objects/supernovae2.html

Life Cycles of Stars
http://imagine.gsfc.nasa.gov/educators/lifecycles/stars.html

Functions: Domain and Range

Functions v. Relations

Purplemath

Let's return to the subject of domains and ranges.

When functions are first introduced, you will probably have some simplistic "functions" and relations to deal with, usually being just sets of points. These won't be terribly useful or interesting functions and relations, but your text wants you to get the idea of what the domain and range of a function are. Small sets of points are generally the simplest sorts of relations, so your book starts with those.

For instance:

 

MathHelp.com

Domain and Range

• State the domain and range of the following relation. Is the relation a function?

{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}

The above list of points, being a relationship between certain x's and certain y's, is a relation. The domain is all the x-values, and the range is all the y-values. To give the domain and the range, I just list the values without duplication:

domain: {2, 3, 4, 6}

range: {–3, –1, 3, 6}

(It is customary to list these values in numerical order, but it is not required. Sets are called "unordered lists", so you can list the numbers in any order you feel like. Just don't duplicate: technically, repetitions are okay in sets, but most instructors would count off for this.)

While the given set does indeed represent a relation (because x's and y's are being related to each other), the set they gave me contains two points with the same x-value: (2, –3) and (2, 3). Since x = 2gives me two possible destinations (that is, two possible y-values), then this relation is not a function.

Note that all I had to do to check whether the relation was a function was to look for duplicate x-values. If you find any duplicate x-values, then the different y-values mean that you do not have a function. Remember: For a relation to be a function, each x-value has to go to one, and only one, y-value.

• State the domain and range of the following relation. Is the relation a function?

{(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}

I'll just list the x-values for the domain and the y-values for the range:

domain: {–3, –2, –1, 0, 1, 2}

range: {5}

This is another example of a "boring" function, just like the example on the previous page: every last x-value goes to the exact same y-value. But each x-value is different, so, while boring,

this relation is indeed a function.

In point of fact, these points lie on the horizontal line y = 5.

---

By the way, the name for a set with only one element in it, like the "range" set above, is "singleton". So the range could also be stated as "the singleton of 5"

---

Content Continues Below

---

There is one other case for finding the domain and range of functions. They will give you a function and ask you to find the domain (and maybe the range, too). I have only ever seen (or can even think of) two things at this stage in your mathematical career that you'll have to check in order to determine the domain of the function they'll give you, and those two things are denominators and square roots.

• Determine the domain and range of the given function:

$\mathbf{\color{green}{\mathit{y} = \dfrac{\mathit{x}^2 + \mathit{x} - 2}{\mathit{x}^2 - \mathit{x} - 2}}}$

The domain is all the values that x is allowed to take on. The only problem I have with this function is that I need to be careful not to divide by zero. So the only values that x can not take on are those which would cause division by zero. So I'll set the denominator equal to zero and solve; my domain will be everything else.

x² – x – 2 = 0

(x – 2)(x + 1) = 0

x = 2 or x = –1

Then the domain is "all x not equal to –1 or 2".

The range is a bit trickier, which is why they may not ask for it. In general, though, they'll want you to graph the function and find the range from the picture. In this case:

As you can see from my picture, the graph "covers" all y-values; that is, the graph will go as low as I like, and will also go as high as I like. For any point on the y-axis, no matter how high up or low down, I can go from that point either to the right or to the left and, eventually, I'll cross the graph. Since the graph will eventually cover all possible values of y, then:

the range is "all real numbers".

• Determine the domain and range of the given function:

$\mathbf{\color{green}{\mathit{y} = -\sqrt{-2\mathit{x} + 3}}}$

Advertisement

The domain is all values that x can take on. The only problem I have with this function is that I cannot have a negative inside the square root. So I'll set the insides greater-than-or-equal-to zero, and solve. The result will be my domain:

–2x + 3 ≥ 0

–2x ≥ –3

2x ≤ 3

x ≤ 3/2 = 1.5

Then the domain is "all x ≤ 3/2".

The range requires a graph. I need to be careful when graphing radicals:

The graph starts at y = 0 and goes down (heading to the left) from there. While the graph goes down very slowly, I know that, eventually, I can go as low as I like (by picking an x that is sufficiently big). Also, from my experience with graphing, I know that the graph will never start coming back up. Then:

the range is "all y ≤ 0".

Affiliate

• Determine the domain and range of the given function:

y = –x⁴ + 4

This is just a garden-variety polynomial. There are no denominators (so no division-by-zero problems) and no radicals (so no square-root-of-a-negative problems). There are no problems with a polynomial. There are no values that I can't plug in for x. When I have a polynomial, the answer for the domain is always:

the domain is "all x".

The range will vary from polynomial to polynomial, and they probably won't even ask, but when they do, I look at the picture:

The graph goes only as high as y = 4, but it will go as low as I like. Then:

The range is "all y ≤ 4"

                      https://www.purplemath.com/modules/fcns2.htm

Week of October 22, 2018

Astronomy

The Life of a Star

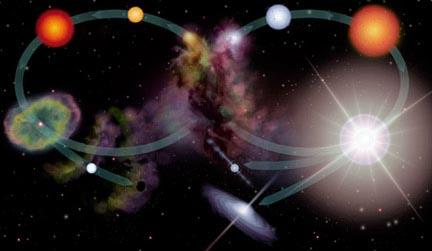
This page (as the title says) is all about the life of a star. It will show all the stages that a small star, and a massive star have to go through during their lifetime. We have all sorts of pics and links for you to look at and explore when you are just about ready to recieve that vast information that we have kindly put together. But we have one FAQ! What is a Star? Stars are hot bodies of glowing gas that start their life in Nebulae. They vary in size, mass and temperature, diameters ranging from 450x smaller to over 1000x larger than that of the Sun. Masses range from a twentieth to over 50 solar masses and surface temperature can range from 3,000 degrees Celcius to over 50,000 degrees Celcius.
The colour of a star is determined by its temperature, the hottest stars are blue and the coolest stars are red. The Sun has a surface temperature of 5,500 degrees Celcius, its colour appears yellow.
The energy produced by the star is by nuclear fusion in the stars core. The brightness is measured in magnitude, the brighter the star the lower the magnitude goes down. There are two ways to measuring the brightness of a star, apparent magnitude is the brghtness seen from Earth, and absolute magnitude which is the brightness of a star seen from a standard distance of 10 parsecs (32.6 light years). Stars can be plotted on a graph using the Hertzsprung Russell Diagram (see picture below).
Hertzsrung Russell Diagram It shows that the temerature coincides with the luminosity, the hotter the star the higher the luminosity the star has. You can also tell the size of each star from the graph as the higher the radius the higher the temperature and luminosity.

---

Small Stars- The Life of a Star of about one Solar Mass. Small stars have a mass upto one and a half times that of the Sun.
Stage 1- Stars are born in a region of high density Nebula, and condenses into a huge globule of gas and dust and contracts under its own gravity.
This image shows the Orion Nebula or M42 . Stage 2 - A region of condensing matter will begin to heat up and start to glow forming Protostars. If a protostar contains enough matter the central temperature reaches 15 million degrees centigrade.
This image is the outflow (coloured red)and protostar. Stage 3 - At this temperature, nuclear reactions in which hydrogen fuses to form helium can start.
Stage 4 - The star begins to release energy, stopping it from contracting even more and causes it to shine. It is now a Main Sequence Star.
The nearest main sequence star to Earth, the Sun Stage 5 - A star of one solar mass remains in main sequence for about 10 billion years, until all of the hydrogen has fused to form helium.
Stage 6 - The helium core now starts to contract further and reactions begin to occur in a shell around the core.
Stage 7 - The core is hot enough for the helium to fuse to form carbon. The outer layers begin to expand, cool and shine less brightly. The expanding star is now called a Red Giant.
The star expands to a Red Giant, below Stage 8 - The helium core runs out, and the outer layers drift of away from the core as a gaseous shell, this gas that surrounds the core is called a Planetary Nebula.
A Planetary Nebula (Below, NGC 6543). Stage 9 - The remaining core (thats 80% of the original star) is now in its final stages. The core becomes a White Dwarf the star eventually cools and dims. When it stops shining, the now dead star is called a Black Dwarf.

---

Massive Stars - The Life of a Star of about 10 Solar Masses Massive stars have a mass 3x times that of the Sun. Some are 50x that of the Sun
Stage 1 - Massive stars evolve in a simlar way to a small stars until it reaces its main sequence stage (see small stars, stages 1-4). The stars shine steadily until the hydrogen has fused to form helium ( it takes billions of years in a small star, but only millions in a massive star).
Stage 2 - The massive star then becomes a Red Supergiant and starts of with a helium core surrounded by a shell of cooling, expanding gas.
The massive star is much bigger in its expanding stage. (A Red Supergiant,below). Stage 3 - In the next million years a series of nuclear reactions occur forming different elements in shells around the iron core.
Stage 4 - The core collapses in less than a second, causing an explosion called a Supernova, in which a shock wave blows of the outer layers of the star. (The actual supernova shines brighter than the entire galaxy for a short time).
The set of images below shows the star going into a stage called Supernova and contracting to become a neutron star The images above were from the HEASARC Homepage Stage 5 - Sometimes the core survives the explosion. If the surviving core is between 1.5 - 3 solar masses it contracts to become a a tiny, very dense Neutron Star. If the core is much greater than 3 solar masses, the core contracts to become a Black Hole.

http://www.astro.keele.ac.uk/workx/starlife/StarpageS_26M.html

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Symbol	Words	Example
>	greater than	x + 3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x − 1
≤	less than or equal to	2y + 1 ≤ 7

Solving

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

Something like:		x < 5
or:		y ≥ 11

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

Simplify:

x > 10

Solved!

How to Solve

Solving inequalities is very like solving equations ... we do most of the same things ...

... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"

Some things can change the direction!

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

3x < 10

But these things do change the direction of the inequality ("<" becomes ">" for example):

Multiply (or divide) both sides by a negative number
Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality:

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:

Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 − 3 < 7 − 3    

x < 4

And that is our solution: x < 4
In other words, x can be any value less than 4.

What did we do?

We went from this: To this:			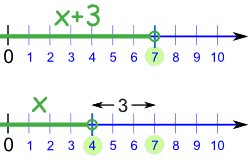	x+3 < 7 x < 4

And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5
If we subtract 5 from both sides, we get:

12 − 5 < x + 5 − 5    

7 < x

That is a solution!
But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number:

Solve: 3y < 15

If we divide both sides by 3 we get:

3y/3 < 15/3

y < 5

And that is our solution: y < 5

Negative Values

When we multiply or divide by a negative number  we must reverse the inequality.

Why?

Well, just look at the number line!

For example, from 3 to 7 is an increase,
but from −3 to −7 is a decrease.

−7 < −3	7 > 3

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Solve: −2y < −8

Let us divide both sides by −2 ... and reverse the inequality!

−2y < −8

−2y/−2 > −8/−2

y > 4

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Solve: bx < 3b

It seems easy just to divide both sides by b, which gives us:

x < 3

... but wait ... if b is negative we need to reverse the inequality like this:

x > 3

But we don't know if b is positive or negative, so we can't answer this one!

To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b:

• if b is 1, then the answer is x < 3
• but if b is −1, then we are solving −x < −3, and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b.

So:

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Solve: x−32 < −5

First, let us clear out the "/2" by multiplying both sides by 2.
Because we are multiplying by a positive number, the inequalities will not change.

x−32 ×2 < −5 ×2  

x−3 < −10

Now add 3 to both sides:

x−3 + 3 < −10 + 3    

x < −7

And that is our solution: x < −7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Solve:

−2 < 6−2x3 < 4

First, let us clear out the "/3" by multiplying each part by 3.
Because we are multiplying by a positive number, the inequalities will not change:

−6 < 6−2x < 12

Now subtract 6 from each part:

−12 < −2x < 6

Now multiply each part by −(1/2).
Because we are multiplying by a negative number, the inequalities change direction.

6 > x >−3

And that is the solution!
But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

−3 < x < 6

Summary

• Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
• But these things will change direction of the inequality:
  • Multiplying or dividing both sides by a negative number
  • Swapping left and right hand sides
• Don't multiply or divide by a variable (unless you know it is always positive or always negative)
• https://www.mathsisfun.com/algebra/inequality-solving.html