Week of October 22, 2018

Astronomy

The Life of a Star

This page (as the title says) is all about the life of a star. It will show all the stages that a small star, and a massive star have to go through during their lifetime. We have all sorts of pics and links for you to look at and explore when you are just about ready to recieve that vast information that we have kindly put together. But we have one FAQ! What is a Star? Stars are hot bodies of glowing gas that start their life in Nebulae. They vary in size, mass and temperature, diameters ranging from 450x smaller to over 1000x larger than that of the Sun. Masses range from a twentieth to over 50 solar masses and surface temperature can range from 3,000 degrees Celcius to over 50,000 degrees Celcius.
The colour of a star is determined by its temperature, the hottest stars are blue and the coolest stars are red. The Sun has a surface temperature of 5,500 degrees Celcius, its colour appears yellow.
The energy produced by the star is by nuclear fusion in the stars core. The brightness is measured in magnitude, the brighter the star the lower the magnitude goes down. There are two ways to measuring the brightness of a star, apparent magnitude is the brghtness seen from Earth, and absolute magnitude which is the brightness of a star seen from a standard distance of 10 parsecs (32.6 light years). Stars can be plotted on a graph using the Hertzsprung Russell Diagram (see picture below).
Hertzsrung Russell Diagram It shows that the temerature coincides with the luminosity, the hotter the star the higher the luminosity the star has. You can also tell the size of each star from the graph as the higher the radius the higher the temperature and luminosity.

---

Small Stars- The Life of a Star of about one Solar Mass. Small stars have a mass upto one and a half times that of the Sun.
Stage 1- Stars are born in a region of high density Nebula, and condenses into a huge globule of gas and dust and contracts under its own gravity.
This image shows the Orion Nebula or M42 . Stage 2 - A region of condensing matter will begin to heat up and start to glow forming Protostars. If a protostar contains enough matter the central temperature reaches 15 million degrees centigrade.
This image is the outflow (coloured red)and protostar. Stage 3 - At this temperature, nuclear reactions in which hydrogen fuses to form helium can start.
Stage 4 - The star begins to release energy, stopping it from contracting even more and causes it to shine. It is now a Main Sequence Star.
The nearest main sequence star to Earth, the Sun Stage 5 - A star of one solar mass remains in main sequence for about 10 billion years, until all of the hydrogen has fused to form helium.
Stage 6 - The helium core now starts to contract further and reactions begin to occur in a shell around the core.
Stage 7 - The core is hot enough for the helium to fuse to form carbon. The outer layers begin to expand, cool and shine less brightly. The expanding star is now called a Red Giant.
The star expands to a Red Giant, below Stage 8 - The helium core runs out, and the outer layers drift of away from the core as a gaseous shell, this gas that surrounds the core is called a Planetary Nebula.
A Planetary Nebula (Below, NGC 6543). Stage 9 - The remaining core (thats 80% of the original star) is now in its final stages. The core becomes a White Dwarf the star eventually cools and dims. When it stops shining, the now dead star is called a Black Dwarf.

---

Massive Stars - The Life of a Star of about 10 Solar Masses Massive stars have a mass 3x times that of the Sun. Some are 50x that of the Sun
Stage 1 - Massive stars evolve in a simlar way to a small stars until it reaces its main sequence stage (see small stars, stages 1-4). The stars shine steadily until the hydrogen has fused to form helium ( it takes billions of years in a small star, but only millions in a massive star).
Stage 2 - The massive star then becomes a Red Supergiant and starts of with a helium core surrounded by a shell of cooling, expanding gas.
The massive star is much bigger in its expanding stage. (A Red Supergiant,below). Stage 3 - In the next million years a series of nuclear reactions occur forming different elements in shells around the iron core.
Stage 4 - The core collapses in less than a second, causing an explosion called a Supernova, in which a shock wave blows of the outer layers of the star. (The actual supernova shines brighter than the entire galaxy for a short time).
The set of images below shows the star going into a stage called Supernova and contracting to become a neutron star The images above were from the HEASARC Homepage Stage 5 - Sometimes the core survives the explosion. If the surviving core is between 1.5 - 3 solar masses it contracts to become a a tiny, very dense Neutron Star. If the core is much greater than 3 solar masses, the core contracts to become a Black Hole.

http://www.astro.keele.ac.uk/workx/starlife/StarpageS_26M.html

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Symbol	Words	Example
>	greater than	x + 3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x − 1
≤	less than or equal to	2y + 1 ≤ 7

Solving

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

Something like:		x < 5
or:		y ≥ 11

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

Simplify:

x > 10

Solved!

How to Solve

Solving inequalities is very like solving equations ... we do most of the same things ...

... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"

Some things can change the direction!

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

3x < 10

But these things do change the direction of the inequality ("<" becomes ">" for example):

Multiply (or divide) both sides by a negative number
Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality:

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:

Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 − 3 < 7 − 3    

x < 4

And that is our solution: x < 4
In other words, x can be any value less than 4.

What did we do?

We went from this: To this:		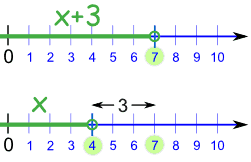		x+3 < 7 x < 4

And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5
If we subtract 5 from both sides, we get:

12 − 5 < x + 5 − 5    

7 < x

That is a solution!
But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number:

Solve: 3y < 15

If we divide both sides by 3 we get:

3y/3 < 15/3

y < 5

And that is our solution: y < 5

Negative Values

When we multiply or divide by a negative number  we must reverse the inequality.

Why?

Well, just look at the number line!

For example, from 3 to 7 is an increase,
but from −3 to −7 is a decrease.

−7 < −3	7 > 3

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Solve: −2y < −8

Let us divide both sides by −2 ... and reverse the inequality!

−2y < −8

−2y/−2 > −8/−2

y > 4

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Solve: bx < 3b

It seems easy just to divide both sides by b, which gives us:

x < 3

... but wait ... if b is negative we need to reverse the inequality like this:

x > 3

But we don't know if b is positive or negative, so we can't answer this one!

To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b:

• if b is 1, then the answer is x < 3
• but if b is −1, then we are solving −x < −3, and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b.

So:

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Solve: x−32 < −5

First, let us clear out the "/2" by multiplying both sides by 2.
Because we are multiplying by a positive number, the inequalities will not change.

x−32 ×2 < −5 ×2  

x−3 < −10

Now add 3 to both sides:

x−3 + 3 < −10 + 3    

x < −7

And that is our solution: x < −7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Solve:

−2 < 6−2x3 < 4

First, let us clear out the "/3" by multiplying each part by 3.
Because we are multiplying by a positive number, the inequalities will not change:

−6 < 6−2x < 12

Now subtract 6 from each part:

−12 < −2x < 6

Now multiply each part by −(1/2).
Because we are multiplying by a negative number, the inequalities change direction.

6 > x >−3

And that is the solution!
But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

−3 < x < 6

Summary

• Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
• But these things will change direction of the inequality:
  • Multiplying or dividing both sides by a negative number
  • Swapping left and right hand sides
• Don't multiply or divide by a variable (unless you know it is always positive or always negative)
• https://www.mathsisfun.com/algebra/inequality-solving.html