Week of November 26,2018

Astronomy

What is a planet?

The planets in our solar system didn’t appear out of nowhere. Neither did the sun. They were all part of a big cloud of gas and dust. Gravity collected lots of material in the center to create the sun. The left over stuff swirled around the forming sun, colliding and collecting together. Some would have enough gravity to attract even more gas and dust, eventually forming planets. Watch this to learn more.

Scientists spent a lot of time arguing over what a planet actually is. In 2006, they came up with a definition. They said a planet must do three things. The first thing might seem obvious—it has to orbit around the sun. Second, it must be big enough to have enough gravity to force it into a spherical shape . And third, it must be big enough that its gravity cleared away any other objects of a similar size near its orbit around the Sun.

What about planets in other places?

This definition is very much focused on our own solar system. But there are also planets in places that are not our solar system. These planets are called exoplanets. They can be found circling around stars, just like the planets here in our own solar system. Does that mean that all planets form the same way? Are all planets made from a star’s leftovers?

That depends on who you talk to. What happens if a small cloud of gas floating out in the middle of nowhere forms a sphere because its gravity? Is that a planet, too? After all, Jupiter is a big sphere of gas. And both are just a mass of stuff that wasn’t quite big enough to form a bright, fiery star.

Big planet or tiny star?

Clouds of gas that don’t have enough material to form a bright star collect into spheres all the time. Most of the time these clouds form a type of star called a brown dwarf. They are pretty big compared to most planets, but they are not big enough to turn into the kind of star that makes lots of energy and gives off light.

https://spaceplace.nasa.gov/planet-what-is/en/

Relative sizes of different planets, our sun, and things in between.

But scientists recently discovered an even smaller gassy object in the middle of nowhere (read more about it here). It appears redder than most brown dwarfs, and is likely much younger than most, too. This object could have formed just like a brown dwarf—from a small cloud of gas. Or maybe it was created around a star and it somehow got flung off into space.

Some scientists are calling this object a planet. Others think that it can only be a planet if it formed around a star. They think that if it just formed from a cloud of gas, then it’s nothing more than a not-quite-star.

Foundations of Algebra

Arithmetic Sequences and Sums

Sequence

A Sequence is a set of things (usually numbers) that are in order.

Each number in the sequence is called a term (or sometimes "element" or "member"), read Sequences and Series for more details.

Arithmetic Sequence

In an Arithmetic Sequence the difference between one term and the next is a constant.

In other words, we just add the same value each time ... infinitely.

Example:

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number.
The pattern is continued by adding 3 to the last number each time, like this:

In General we could write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

where:

• a is the first term, and
• d is the difference between the terms (called the "common difference")

Example: (continued)

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

Has:

• a = 1 (the first term)
• d = 3 (the "common difference" between terms)

And we get:

{a, a+d, a+2d, a+3d, ... }

{1, 1+3, 1+2×3, 1+3×3, ... }

{1, 4, 7, 10, ... }

Rule

We can write an Arithmetic Sequence as a rule:

x_n = a + d(n−1)

(We use "n−1" because d is not used in the 1st term).

Example: Write a rule, and calculate the 9th term, for this Arithmetic Sequence:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.

The values of a and d are:

• a = 3 (the first term)
• d = 5 (the "common difference")

Using the Arithmetic Sequence rule:

x_n = a + d(n−1)

= 3 + 5(n−1)

= 3 + 5n − 5

= 5n − 2

So the 9th term is:

x₉ = 5×9 − 2
= 43

Is that right? Check for yourself!

Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)

Advanced Topic: Summing an Arithmetic Series

To sum up the terms of this arithmetic sequence:

a + (a+d) + (a+2d) + (a+3d) + ...

use this formula:

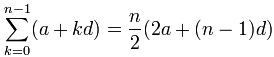
What is that funny symbol? It is called Sigma Notation

(called Sigma) means "sum up"

And below and above it are shown the starting and ending values:

It says "Sum up n where n goes from 1 to 4. Answer=10

Here is how to use it:

Example: Add up the first 10 terms of the arithmetic sequence:

{ 1, 4, 7, 10, 13, ... }

The values of a, d and n are:

• a = 1 (the first term)
• d = 3 (the "common difference" between terms)
• n = 10 (how many terms to add up)

So:

Becomes:

= 5(2+9·3) = 5(29) = 145

Check: why don't you add up the terms yourself, and see if it comes to 145

Footnote: Why Does the Formula Work?

Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

First, we will call the whole sum "S":

S = a + (a + d) + ... + (a + (n−2)d) + (a + (n−1)d)

Next, rewrite S in reverse order:

S = (a + (n−1)d) + (a + (n−2)d) + ... + (a + d) + a

Now add those two, term by term:

S	=	a	+	(a+d)	+	...	+	(a + (n-2)d)	+	(a + (n-1)d)
S	=	(a + (n-1)d)	+	(a + (n-2)d)	+	...	+	(a + d)	+	a
2S	=	(2a + (n-1)d)	+	(2a + (n-1)d)	+	...	+	(2a + (n-1)d)	+	(2a + (n-1)d)

Each term is the same! And there are "n" of them so ...

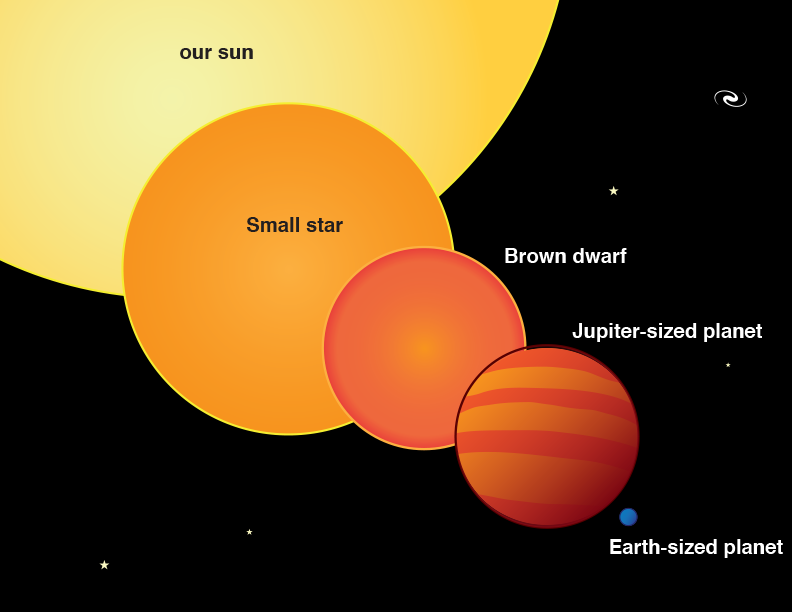
2S = n × (2a + (n−1)d)

Now, just divide by 2 and we get:

S = (n/2) × (2a + (n−1)d)

Which is our formula:

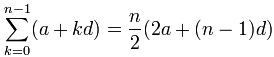
https://www.mathsisfun.com/algebra/sequences-sums-arithmetic.html