Factoring in Algebra
Factors
Numbers have factors:

And expressions (like x2+4x+3) also have factors:

Factoring
Factoring (called "Factorising" in the UK) is the process of finding the factors:
Factoring: Finding what to multiply together to get an expression.
It is like "splitting" an expression into a multiplication of simpler expressions.
Factoring is also the opposite of Expanding:

Common Factor
In the previous example we saw that 2y and 6 had a common factor of 2
But to do the job properly we need the highest common factor, including any variables
More Complicated Factoring
Factoring Can Be Hard !
The examples have been simple so far, but factoring can be very tricky.
Because we have to figure what got multiplied to produce the expression we are given!
It is like trying to find which ingredients
went into a cake to make it so delicious.
It can be hard to figure out!
Experience Helps
With more experience factoring becomes easier.
How can you learn to do that? By getting lots of practice, and knowing "Identities"!
Remember these Identities
Here is a list of common "Identities" (including the "difference of squares" used above).
It is worth remembering these, as they can make factoring easier.
 | ||
| a2 − b2 | = | (a+b)(a−b) |
| a2 + 2ab + b2 | = | (a+b)(a+b) |
| a2 − 2ab + b2 | = | (a−b)(a−b) |
| a3 + b3 | = | (a+b)(a2−ab+b2) |
| a3 − b3 | = | (a−b)(a2+ab+b2) |
| a3+3a2b+3ab2+b3 | = | (a+b)3 |
| a3−3a2b+3ab2−b3 | = | (a−b)3 |
There are many more like those, but those are the most useful ones.
Advice
The factored form is usually best.
When trying to factor, follow these steps:
- "Factor out" any common terms
- See if it fits any of the identities, plus any more you may know
- Keep going till you can't factor any more
There are also Computer Algebra Systems (called "CAS") such as Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce and many more that are good at factoring.
More Examples
Experience does help, so here are more examples to help you on the way:
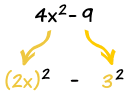
No comments:
Post a Comment