Week of March 2, 2020 College Readiness Math

Point-Slope Equation of a Line

The "point-slope" form of the equation of a straight line is:

y − y₁ = m(x − x₁)

The equation is useful when we know:

• one point on the line: (x₁,y₁)
• and the slope of the line: m,

and want to find other points on the line.

Have a play with it first (move the point, try different slopes):

y − 6 = 0.5(x − 8)

Slope:

0.5

© 2018 MathsIsFun.com v0.891

Now let's discover more.

What does it stand for?

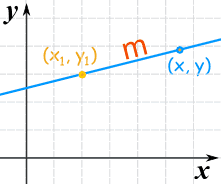
(x₁, y₁) is a known point

m is the slope of the line

(x, y) is any other point on the line

Making sense of it

It is based on the slope:

Slope m  =  change in ychange in x  =  y − y₁x − x₁

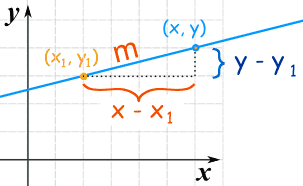
Starting with the slope: we rearrange it like this: to get this: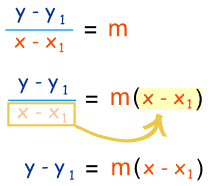

So, it is just the slope formula in a different way!

Now let us see how to use it.

Example 1:

slope "m"  =  31  =  3

y − y₁ = m(x − x₁)

We know m, and also know that (x₁, y₁) = (3,2), and so we have:

y − 2 = 3(x − 3)

That is a perfectly good answer, but we can simplify it a little:

y − 2 = 3x − 9

y = 3x − 9 + 2

y = 3x − 7

Example 2:

m = −31 = −3

y − y₁ = m(x − x₁)

We can pick any point for (x₁, y₁), so let's choose (0,0), and we have:

y − 0 = −3(x − 0)

Which can be simplified to:

y = −3x

Example 3: Vertical Line

What is the equation for a vertical line?
The slope is undefined!

In fact, this is a special case, and we use a different equation, like this:

x = 1.5

Every point on the line has x coordinate 1.5,
that’s why its equation is x = 1.5

What About y = mx + b ?

You may already be familiar with the "y=mx+b" form (called the slope-intercept form of the equation of a line).

It is the same equation, in a different form!

The "b" value (called the y-intercept) is where the line crosses the y-axis.

So point (x₁, y₁) is actually at (0, b)

and the equation becomes:

Start withy − y₁ = m(x − x₁)

(x₁, y₁) is actually (0, b):y − b = m(x − 0)

Which is:y − b = mx

Put b on other side:y = mx + b

source: https://www.mathsisfun.com/algebra/line-equation-point-slope.html