Week of October 23

Happy homecoming week!!

Foundations

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Symbol	Words	Example
>	greater than	x + 3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x - 1
≤	less than or equal to	2y + 1 ≤ 7

Solving

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

Something like:		x < 5
or:		y ≥ 11

We call that "solved".

Example: x + 2 > 12

Subtract 2 from both sides:

x + 2 − 2 > 12 − 2

Simplify:

x > 10

Solved!

How to Solve

Solving inequalities is very like solving equations ... we do most of the same things ...

... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"

Some things can change the direction!

< becomes >

> becomes <

≤ becomes ≥

≥ becomes ≤

Safe Things To Do

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

3x < 10

But these things do change the direction of the inequality ("<" becomes ">" for example):

Multiply (or divide) both sides by a negative number
Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality:

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:

Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 - 3 < 7 - 3    

x < 4

And that is our solution: x < 4
In other words, x can be any value less than 4.

What did we do?

We went from this: To this:		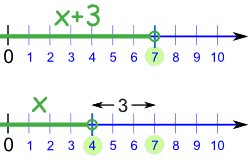		x+3 < 7 x < 4

And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5
If we subtract 5 from both sides, we get:

12 - 5 < x + 5 - 5    

7 < x

That is a solution!
But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number:

Solve: 3y < 15

If we divide both sides by 3 we get:

3y/3 < 15/3

y < 5

And that is our solution: y < 5

Negative Values

When we multiply or divide by a negative number  we must reverse the inequality.

Why?

Well, just look at the number line!

For example, from 3 to 7 is an increase,
but from -3 to -7 is a decrease.

-7 < -3	7 > 3

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Solve: -2y < -8

Let us divide both sides by -2 ... and reverse the inequality!

-2y < -8

-2y/-2 > -8/-2

y > 4

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Solve: bx < 3b

It seems easy just to divide both sides by b, which gives us:

x < 3

... but wait ... if b is negative we need to reverse the inequality like this:

x > 3

But we don't know if b is positive or negative, so we can't answer this one!

To help you understand, imagine replacing b with 1 or -1 in the example of bx < 3b:

• if b is 1, then the answer is x < 3
• but if b is -1, then we are solving -x < -3, and the answer is x > 3

The answer could be x < 3 or x > 3 and we can't choose because we don't know b.

So:

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Solve: (x-3)/2 < -5

First, let us clear out the "/2" by multiplying both sides by 2.
Because we are multiplying by a positive number, the inequalities will not change.

(x-3)/2 ×2 < -5 ×2  

(x-3) < -10

Now add 3 to both sides:

x-3 + 3 < -10 + 3    

x < -7

And that is our solution: x < -7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Solve:

-2 < (6-2x)/3 < 4

First, let us clear out the "/3" by multiplying each part by 3:
Because we are multiplying by a positive number, the inequalities will not change.

-6 < 6-2x < 12

Now subtract 6 from each part:

-12 < -2x < 6

Now multiply each part by -(1/2).
Because we are multiplying by a negative number, the inequalities change direction.

6 > x > -3

And that is the solution!
But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

-3 < x < 6

ANATOMY

Nose and Nasal Cavity
The nose and nasal cavity form the main external opening for the respiratory system and are the first section of the body’s airway—the respiratory tract through which air moves. The nose is a structure of the face made of cartilage, bone, muscle, and skin that supports and protects the anterior portion of the nasal cavity. The nasal cavity is a hollow space within the nose and skull that is lined with hairs and mucus membrane. The function of the nasal cavity is to warm, moisturize, and filter air entering the body before it reaches the lungs. Hairs and mucus lining the nasal cavity help to trap dust, mold, pollen and other environmental contaminants before they can reach the inner portions of the body. Air exiting the body through the nose returns moisture and heat to the nasal cavity before being exhaled into the environment.

Mouth
The mouth, also known as the oral cavity, is the secondary external opening for the respiratory tract. Most normal breathing takes place through the nasal cavity, but the oral cavity can be used to supplement or replace the nasal cavity’s functions when needed. Because the pathway of air entering the body from the mouth is shorter than the pathway for air entering from the nose, the mouth does not warm and moisturize the air entering the lungs as well as the nose performs this function. The mouth also lacks the hairs and sticky mucus that filter air passing through the nasal cavity. The one advantage of breathing through the mouth is that its shorter distance and larger diameter allows more air to quickly enter the body.

Pharynx
The pharynx, also known as the throat, is a muscular funnel that extends from the posterior end of the nasal cavity to the superior end of the esophagus and larynx. The pharynx is divided into 3 regions: the nasopharynx, oropharynx, and laryngopharynx. The nasopharynx is the superior region of the pharynx found in the posterior of the nasal cavity. Inhaled air from the nasal cavity passes into the nasopharynx and descends through the oropharynx, located in the posterior of the oral cavity. Air inhaled through the oral cavity enters the pharynx at the oropharynx. The inhaled air then descends into the laryngopharynx, where it is diverted into the opening of the larynx by the epiglottis. The epiglottis is a flap of elastic cartilage that acts as a switch between the trachea and the esophagus. Because the pharynx is also used to swallow food, the epiglottis ensures that air passes into the trachea by covering the opening to the esophagus. During the process of swallowing, the epiglottis moves to cover the trachea to ensure that food enters the esophagus and to prevent choking.

Larynx

The larynx, also known as the voice box, is a short section of the airway that connects the laryngopharynx and the trachea. The larynx is located in the anterior portion of the neck, just inferior to the hyoid bone and superior to the trachea. Several cartilage structures make up the larynx and give it its structure. The epiglottis is one of the cartilage pieces of the larynx and serves as the cover of the larynx during swallowing. Inferior to the epiglottis is the thyroid cartilage, which is often referred to as the Adam’s apple as it is most commonly enlarged and visible in adult males. The thyroid holds open the anterior end of the larynx and protects the vocal folds. Inferior to the thyroid cartilage is the ring-shaped cricoid cartilage which holds the larynx open and supports its posterior end. In addition to cartilage, the larynx contains special structures known as vocal folds, which allow the body to produce the sounds of speech and singing. The vocal folds are folds of mucous membrane that vibrate to produce vocal sounds. The tension and vibration speed of the vocal folds can be changed to change the pitch that they produce.

Trachea
The trachea, or windpipe, is a 5-inch long tube made of C-shaped hyaline cartilage rings lined with pseudostratified ciliated columnar epithelium. The trachea connects the larynx to the bronchi and allows air to pass through the neck and into the thorax. The rings of cartilage making up the trachea allow it to remain open to air at all times. The open end of the cartilage rings faces posteriorly toward the esophagus, allowing the esophagus to expand into the space occupied by the trachea to accommodate masses of food moving through the esophagus.

The main function of the trachea is to provide a clear airway for air to enter and exit the lungs. In addition, the epithelium lining the trachea produces mucus that traps dust and other contaminants and prevents it from reaching the lungs. Cilia on the surface of the epithelial cells move the mucus superiorly toward the pharynx where it can be swallowed and digested in the gastrointestinal tract.

Bronchi and Bronchioles
At the inferior end of the trachea, the airway splits into left and right branches known as the primary bronchi. The left and right bronchi run into each lung before branching off into smaller secondary bronchi. The secondary bronchi carry air into the lobes of the lungs—2 in the left lung and 3 in the right lung. The secondary bronchi in turn split into many smaller tertiary bronchi within each lobe. The tertiary bronchi split into many smaller bronchioles that spread throughout the lungs. Each bronchiole further splits into many smaller branches less than a millimeter in diameter called terminal bronchioles. Finally, the millions of tiny terminal bronchioles conduct air to the alveoli of the lungs.

As the airway splits into the tree-like branches of the bronchi and bronchioles, the structure of the walls of the airway begins to change. The primary bronchi contain many C-shaped cartilage rings that firmly hold the airway open and give the bronchi a cross-sectional shape like a flattened circle or a letter D. As the bronchi branch into secondary and tertiary bronchi, the cartilage becomes more widely spaced and more smooth muscle and elastin protein is found in the walls. The bronchioles differ from the structure of the bronchi in that they do not contain any cartilage at all. The presence of smooth muscles and elastin allow the smaller bronchi and bronchioles to be more flexible and contractile.

The main function of the bronchi and bronchioles is to carry air from the trachea into the lungs. Smooth muscle tissue in their walls helps to regulate airflow into the lungs. When greater volumes of air are required by the body, such as during exercise, the smooth muscle relaxes to dilate the bronchi and bronchioles. The dilated airway provides less resistance to airflow and allows more air to pass into and out of the lungs. The smooth muscle fibers are able to contract during rest to prevent hyperventilation. The bronchi and bronchioles also use the mucus and cilia of their epithelial lining to trap and move dust and other contaminants away from the lungs.

Lungs
The lungs are a pair of large, spongy organs found in the thorax lateral to the heart and superior to the diaphragm. Each lung is surrounded by a pleural membrane that provides the lung with space to expand as well as a negative pressure space relative to the body’s exterior. The negative pressure allows the lungs to passively fill with air as they relax. The left and right lungs are slightly different in size and shape due to the heart pointing to the left side of the body. The left lung is therefore slightly smaller than the right lung and is made up of 2 lobes while the right lung has 3 lobes.

The interior of the lungs is made up of spongy tissues containing many capillaries and around 30 million tiny sacs known as alveoli. The alveoli are cup-shaped structures found at the end of the terminal bronchioles and surrounded by capillaries. The alveoli are lined with thin simple squamous epithelium that allows air entering the alveoli to exchange its gases with the blood passing through the capillaries.

Muscles of Respiration
Surrounding the lungs are sets of muscles that are able to cause air to be inhaled or exhaled from the lungs. The principal muscle of respiration in the human body is the diaphragm, a thin sheet of skeletal muscle that forms the floor of the thorax. When the diaphragm contracts, it moves inferiorly a few inches into the abdominal cavity, expanding the space within the thoracic cavity and pulling air into the lungs. Relaxation of the diaphragm allows air to flow back out the lungs during exhalation.

Between the ribs are many small intercostal muscles that assist the diaphragm with expanding and compressing the lungs. These muscles are divided into 2 groups: the internal intercostal muscles and the external intercostal muscles. The internal intercostal muscles are the deeper set of muscles and depress the ribs to compress the thoracic cavity and force air to be exhaled from the lungs. The external intercostals are found superficial to the internal intercostals and function to elevate the ribs, expanding the volume of the thoracic cavity and causing air to be inhaled into the lungs.

Pulmonary Ventilation
Pulmonary ventilation is the process of moving air into and out of the lungs to facilitate gas exchange. The respiratory system uses both a negative pressure system and the contraction of muscles to achieve pulmonary ventilation. The negative pressure system of the respiratory system involves the establishment of a negative pressure gradient between the alveoli and the external atmosphere. The pleural membrane seals the lungs and maintains the lungs at a pressure slightly below that of the atmosphere when the lungs are at rest. This results in air following the pressure gradient and passively filling the lungs at rest. As the lungs fill with air, the pressure within the lungs rises until it matches the atmospheric pressure. At this point, more air can be inhaled by the contraction of the diaphragm and the external intercostal muscles, increasing the volume of the thorax and reducing the pressure of the lungs below that of the atmosphere again. 

To exhale air, the diaphragm and external intercostal muscles relax while the internal intercostal muscles contract to reduce the volume of the thorax and increase the pressure within the thoracic cavity. The pressure gradient is now reversed, resulting in the exhalation of air until the pressures inside the lungs and outside of the body are equal. At this point, the elastic nature of the lungs causes them to recoil back to their resting volume, restoring the negative pressure gradient present during inhalation.

External Respiration
External respiration is the exchange of gases between the air filling the alveoli and the blood in the capillaries surrounding the walls of the alveoli. Air entering the lungs from the atmosphere has a higher partial pressure of oxygen and a lower partial pressure of carbon dioxide than does the blood in the capillaries. The difference in partial pressures causes the gases to diffuse passively along their pressure gradients from high to low pressure through the simple squamous epithelium lining of the alveoli. The net result of external respiration is the movement of oxygen from the air into the blood and the movement of carbon dioxide from the blood into the air. The oxygen can then be transported to the body’s tissues while carbon dioxide is released into the atmosphere during exhalation.

Internal Respiration
Internal respiration is the exchange of gases between the blood in capillaries and the tissues of the body. Capillary blood has a higher partial pressure of oxygen and a lower partial pressure of carbon dioxide than the tissues through which it passes. The difference in partial pressures leads to the diffusion of gases along their pressure gradients from high to low pressure through the endothelium lining of the capillaries. The net result of internal respiration is the diffusion of oxygen into the tissues and the diffusion of carbon dioxide into the blood.

Transportation of Gases
The 2 major respiratory gases, oxygen and carbon dioxide, are transported through the body in the blood. Blood plasma has the ability to transport some dissolved oxygen and carbon dioxide, but most of the gases transported in the blood are bonded to transport molecules. Hemoglobin is an important transport molecule found in red blood cells that carries almost 99% of the oxygen in the blood. Hemoglobin can also carry a small amount of carbon dioxide from the tissues back to the lungs. However, the vast majority of carbon dioxide is carried in the plasma as bicarbonate ion. When the partial pressure of carbon dioxide is high in the tissues, the enzyme carbonic anhydrase catalyzes a reaction between carbon dioxide and water to form carbonic acid. Carbonic acid then dissociates into hydrogen ion and bicarbonate ion. When the partial pressure of carbon dioxide is low in the lungs, the reactions reverse and carbon dioxide is liberated into the lungs to be exhaled.

Homeostatic Control of Respiration
Under normal resting conditions, the body maintains a quiet breathing rate and depth called eupnea. Eupnea is maintained until the body’s demand for oxygen and production of carbon dioxide rises due to greater exertion. Autonomic chemoreceptors in the body monitor the partial pressures of oxygen and carbon dioxide in the blood and send signals to the respiratory center of the brain stem. The respiratory center then adjusts the rate and depth of breathing to return the blood to its normal levels of gas partial pressures.

http://www.innerbody.com/anatomy/respiratory

GEOMETRY

Surface Area and Volume of a Sphere

D. Russell

A three-dimensional circle is known as a sphere. In order to calculate either the surface area or the volume of a sphere, you need to know the radius (r). The radius is the distance from the center of the sphere to the edge and it is always the same, no matter which points on the sphere's edge you measure from.

Once you have the radius, the formulas are rather simple to remember. Just as with ​the circumference of the circle, you will need to use pi (π). Generally, you can round this infinite number to 3.14 or 3.14159 (the accepted fraction is 22/7).

• Surface Area = 4πr²
• Volume = 4/3 πr³

02

of 16

Surface Area and Volume of a Cone

D. Russell

A cone is a pyramid with a circular base that has sloping sides which meet at a central point. In order to calculate its surface area or volume, you must know the radius of the base and the length of the side.

If you do not know it, you can find the side length (s) using the radius (r) and the cone's height (h).

• s = √(r2 + h2)

With that, you can then find the total surface area, which is the sum of the area of the base and area of the side.

• Area of Base: πr²
• Area of Side: πrs
• Total Surface Area = πr² + πrs

To find the volume of a sphere, you only need the radius and the height.

• Volume = 1/3 πr²h

03

of 16

Surface Area and Volume of a Cylinder

D. Russell

You will find that a cylinder is much easier to work with than a cone. This shape has a circular base and straight, parallel sides. This means that in order to find its surface area or volume, you only need the radius (r) and height (h).

However, you must also factor in that there is both a top and a bottom, which is why the radius must be multiplied by two for the surface area.

• Surface Area = 2πr² + 2πrh
• Volume = πr²h

04

of 16

Surface Area and Volume of a Rectangular Prism

D. Russell

A rectangular in three dimensions becomes a rectangular prism (or a box). When all sides are of equal dimensions, it becomes a cube. Either way, finding the surface area and the volume require the same formulas.

For these, you will need to know the length (l), the height (h), and the width (w). With a cube, all three will be the same.

• Surface Area = 2(lh) + 2(lw) + 2(wh)
• Volume = lhw

05

of 16

Surface Area and Volume of a Pyramid

D. Russell

A pyramid with a square base and faces made of equilateral triangles is relatively easy to work with.

You will need to know the measurement for one length of the base (b). The height (h) is the distance from the base to the center point of the pyramid. The side (s) is the length of one face of the pyramid, from the base to the top point.

• Surface Area = 2bs + b²
• Volume = 1/3 b²h

Another way to calculate this is to use the perimeter (P) and the area (A) of the base shape. This can be used on a pyramid that has a rectangular rather than a square base.

• Surface Area = ( ½ x P x s ) + A
• Volume = 1/3 Ah

06

of 16

Surface Area and Volume of a Prism

D. Russell

When you switch from a pyramid to an isosceles triangular prism, you must also factor in the length (l) of the shape. Remember the abbreviations for base (b), height (h), and side (s) because they are needed for these calculations.

• Surface Area = bh + 2ls + lb
• Volume = 1/2 (bh)l

Yet, a prism can be any stack of shapes. If you have to determine the area or volume of an odd prism, you can rely on the area (A) and the perimeter (P) of the base shape. Many times, this formula will use the height of the prism, or depth (d), rather than the length (l), though you may see either abbreviation.

• Surface Area = 2A + Pd
• Volume = Ad

07

of 16

Area of a Circle Sector

D. Russell

The area of a sector of a circle can be calculated by degrees (or radians as is used more often in calculus). For this, you will need the radius (r), pi (π), and the central angle (θ).

https://www.thoughtco.com/surface-area-and-volume-2312247