Algebra 2
Complex Numbers

A Complex Number
A Complex Number is a combination of a
Real Number and an Imaginary Number
Nearly any number you can think of is a Real Number!
Normally this doesn't happen, because:
But just imagine such numbers exist, because we will need them.
The "unit" imaginary number (like
1 for Real Numbers) is
i, which is the square root of −1
Because when we square
i we get
−1
i2 = −1
Examples of Imaginary Numbers:
| 3i | 1.04i | −2.8i | 3i/4 | (√2)i | 1998i |
And we keep that little "i" there to remind us we need to multiply by √−1
Complex Numbers
A Complex Number is a combination of a Real Number and an Imaginary Number:
Examples:
| 1 + i | 39 + 3i | 0.8 − 2.2i | −2 + πi | √2 + i/2 |
Can a Number be a Combination of Two Numbers?
Can we make up a number from two other numbers? Sure we can!
We do it with
fractions all the time. The fraction
3/8 is a number made up of a 3 and an 8. We know it means "3 of 8 equal parts".
Well, a Complex Number is just two numbers added together (a Real and an Imaginary Number).
Either Part Can Be Zero
So, a Complex Number has a real part and an imaginary part.
But either part can be 0, so all Real Numbers and Imaginary Numbers are also Complex Numbers.
| Complex Number | Real Part | Imaginary Part |
|---|
| 3 + 2i | 3 | 2 |
| 5 | 5 | 0 |
| −6i | 0 | −6 |
Complicated?
Complex does not mean complicated.
It means the two types of numbers, real and imaginary, together form a complex, just like a building complex (buildings joined together).
A Visual Explanation
You know how the number line goes left-right?
Well let's have the imaginary numbers go up-down:
A complex number can now be shown as a point:

The complex number 3 + 4
i
Adding
To add two complex numbers we add each part separately:
(a+bi) + (c+di) = (a+c) + (b+d)i
Example: add the complex numbers 3 + 2i and 1 + 7i
- add the real numbers, and
- add the imaginary numbers:
(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7)i
= 4 + 9i
Let's try another:
Example: add the complex numbers 3 + 5i and 4 − 3i
(3 + 5i) + (4 − 3i)
= 3 + 4 + (5 − 3)i
= 7 + 2i
On the complex plane it is:
Multiplying
To multiply complex numbers:
Each part of the first complex number gets multiplied by
each part of the second complex number
 |
- Firsts: a × c
- Outers: a × di
- Inners: bi × c
- Lasts: bi × di
|
(a+bi)(c+di) = ac + adi + bci + bdi2
|
Like this:
Example: (3 + 2i)(1 + 7i)
(3 + 2i)(1 + 7i)= 3×1 + 3×7i + 2i×1+ 2i×7i
= 3 + 21i + 2i + 14i2
= 3 + 21i + 2i − 14 (because i2 = −1)
= −11 + 23i
And this:
Example: (1 + i)2
(1 + i)(1 + i)= 1×1 + 1×i + 1×i + i2
= 1 + 2i − 1 (because i2 = −1)
= 0 + 2i
But There is a Quicker Way!
Use this rule:
(a+bi)(c+di) = (ac−bd) + (ad+bc)i
Example: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i
Why Does That Rule Work?
It is just the "FOIL" method after a little work:
(a+bi)(c+di) =ac + adi + bci + bdi2 FOIL method
=ac + adi + bci − bd (because i2 = −1)
=(ac − bd) + (ad + bc)i (gathering like terms)
And there we have the (ac − bd) + (ad + bc)i pattern.
This rule is certainly faster, but if you forget it, just remember the FOIL method.
Let us try i2
Just for fun, let's use the method to calculate i2
Example: i2
We can write
i with a real and imaginary part as
0 + i
i2 = (0 + i)2= (0 + i)(0 + i)
= (0×0 − 1×1) + (0×1 + 1×0)i
= −1 + 0i
= −1
And that agrees nicely with the definition that i2 = −1
So it all works wonderfully!
Conjugates
We will need to know about conjugates in a minute!
A
conjugate is where we
change the sign in the middle like this:
A conjugate is often written with a bar over it:
Dividing
The conjugate is used to help complex division.
The trick is to multiply both top and bottom by the conjugate of the bottom.
Example: Do this Division:
2 + 3i4 − 5i
Multiply top and bottom by the conjugate of
4 − 5i :
2 + 3i4 − 5i×4 + 5i4 + 5i = 8 + 10i + 12i + 15i216 + 20i − 20i − 25i2
Now remember that
i2 = −1, so:
= 8 + 10i + 12i − 1516 + 20i − 20i + 25
Add Like Terms (and notice how on the bottom
20i − 20i cancels out!):
= −7 + 22i41
Lastly we should put the answer back into
a + bi form:
= −7 41 + 2241i
DONE!
Yes, there is a bit of calculation to do. But it can be done.
Multiplying By the Conjugate
There is a faster way though.
In the previous example, what happened on the bottom was interesting:
(4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i2
The middle terms (20i − 20i) cancel out! Also i2 = −1 so we end up with this:
(4 − 5i)(4 + 5i) = 42 + 52
Which is really quite a simple result. The general rule is:
(a + bi)(a − bi) = a2 + b2
We can use that to save us time when do division, like this:
Example: Let's try this again
2 + 3i4 − 5i
Multiply top and bottom by the conjugate of 4 − 5i :
2 + 3i4 − 5i×4 + 5i4 + 5i = 8 + 10i + 12i + 15i216 + 25
= −7 + 22i41
And then back into a + bi form:
= −7 41 + 2241i
DONE!
https://www.mathsisfun.com/numbers/complex-numbers.html
Algebra 1
Solving Inequalities
Symbol
|
Words
|
Example
|
|---|
| | |
| > |
greater than
|
x + 3 > 2
|
| < |
less than
|
7x < 28
|
| ≥ |
greater than or equal to
|
5 ≥ x - 1
|
| ≤ |
less than or equal to
|
2y + 1 ≤ 7
|
| | |
Solving
Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:
| Something like: | | x < 5 |
| or: | | y ≥ 11 |
We call that "solved".
Example: x + 2 > 12
Subtract 2 from both sides:
x + 2 − 2 > 12 − 2
Simplify:
x > 10
Solved!
How to Solve
Solving inequalities is very like
solving equations ... we do most of the same things ...
... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"
Some things can change the direction!
< becomes >
> becomes <
≤ becomes ≥
≥ becomes ≤
Safe Things To Do
These things do not affect the direction of the inequality:
- Add (or subtract) a number from both sides
- Multiply (or divide) both sides by a positive number
- Simplify a side
Example: 3x < 7+3
We can simplify 7+3 without affecting the inequality:
3x < 10
But these things do change the direction of the inequality ("<" becomes ">" for example):
Example: 2y+7 < 12
When we swap the left and right hand sides, we must also
change the direction of the inequality:
12 > 2y+7
Here are the details:
Adding or Subtracting a Value
We can often solve inequalities by adding (or subtracting) a number from both sides (just as in
Introduction to Algebra), like this:
Solve: x + 3 < 7
If we subtract 3 from both sides, we get:
x + 3 - 3 < 7 - 3
x < 4
And that is our solution:
x < 4
In other words,
x can be any value less than 4.
What did we do?
We went from this:
To this:
| | 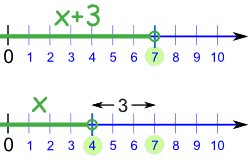 | |
x+3 < 7
x < 4
|
| | | | | |
And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality
Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.
What If I Solve It, But "x" Is On The Right?
No matter, just swap sides, but reverse the sign so it still "points at" the correct value!
Example:
12 < x + 5
If we subtract 5 from both sides, we get:
12 - 5 < x + 5 - 5
7 < x
That is a solution!
But it is normal to put "x" on the left hand side ...
... so let us flip sides (and the inequality sign!):
x > 7
Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution:
x > 7
Note: "x" can be on the right, but people usually like to see it on the left hand side.
Multiplying or Dividing by a Value
But we need to be a bit more careful (as you will see).
Positive Values
Everything is fine if we want to multiply or divide by a positive number:
Solve: 3y < 15
If we divide both sides by 3 we get:
3y/3 < 15/3
y < 5
And that is our solution:
y < 5
Negative Values
 | When we multiply or divide by a negative number
we must reverse the inequality. |
Why?
Well, just look at the number line!
For example, from 3 to 7 is an increase,
but from -3 to -7 is a decrease.
 |
| -7 < -3 | 7 > 3 |
See how the inequality sign reverses (from < to >) ?
Let us try an example:
Solve: -2y < -8
Let us divide both sides by -2 ... and
reverse the inequality!
-2y < -8
-2y/-2 > -8/-2
y > 4
And that is the correct solution:
y > 4
(Note that I reversed the inequality on the same line I divided by the negative number.)
So, just remember:
When multiplying or dividing by a negative number, reverse the inequality
Multiplying or Dividing by Variables
Here is another (tricky!) example:
Solve: bx < 3b
It seems easy just to divide both sides by
b, which gives us:
x < 3
... but wait ... if
b is
negative we need to reverse the inequality like this:
x > 3
But we don't know if b is positive or negative, so
we can't answer this one!
To help you understand, imagine replacing b with 1 or -1 in the example of bx < 3b:
- if b is 1, then the answer is x < 3
- but if b is -1, then we are solving -x < -3, and the answer is x > 3
The answer could be x < 3 or x > 3 and we can't choose because we don't know b.
So:
Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).
A Bigger Example
Solve: (x-3)/2 < -5
First, let us clear out the "/2" by multiplying both sides by 2.
Because we are multiplying by a positive number, the inequalities will not change.
(x-3)/2 ×2 < -5 ×2
(x-3) < -10
Now add 3 to both sides:
x-3 + 3 < -10 + 3
x < -7
And that is our solution:
x < -7
Two Inequalities At Once!
How do we solve something with two inequalities at once?
Solve:
-2 < (6-2x)/3 < 4
First, let us clear out the "/3" by multiplying each part by 3:
Because we are multiplying by a positive number, the inequalities will not change.
-6 < 6-2x < 12
Now subtract 6 from each part:
-12 < -2x < 6
Now multiply each part by -(1/2).
Because we are multiplying by a
negative number, the inequalities
change direction.
6 > x > -3
And that is the solution!
But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):
-3 < x < 6
Summary
- Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
- But these things will change direction of the inequality:
- Multiplying or dividing both sides by a negative number
- Swapping left and right hand sides
- Don't multiply or divide by a variable (unless you know it is always positive or always negative)
https://www.mathsisfun.com/algebra/inequality-solving.html

 Because when we square i we get −1
Because when we square i we get −1










No comments:
Post a Comment