Week of February 5, 2018

Algebra 2

Operations with Polynomials

Learning Objective(s)

·         Add polynomials with more than one variable.

·         Subtract polynomials with more than one variable.

·         Multiply polynomials with more than one variable.

·         Divide polynomials with more than one variable.

Introduction

Just as you can perform the four operations on polynomials with one variable, you can add, subtract, multiply, and divide polynomials with more than one variable. The process is exactly the same, but you have more variables to keep track of. When you are adding and subtracting polynomials with more than one variable, you have to pay particular care to combining like terms only. When you multiply and divide, you also need to pay particular attention to the multiple variables and terms. You can multiply and divide terms that aren’t like, but to add and subtract terms they must be like terms.

Adding Polynomials with More Than One Variable

To add polynomials, you first need to identify the like terms in the polynomials and then combine them according to the correct integer operations. Since like terms must have the same exact variables raised to the same exact power, identifying them in polynomials with more than one variable takes a careful eye. Sometimes parentheses are used to distinguish between the addition of two polynomials and the addition of a collection of monomials. With addition, you can simply remove the parentheses and perform the addition.

Example
Problem		Add. (4x2 – 12xy + 9y2) + (25x2 + 4xy – 32y2)
	4x2 +(−12xy) + 9y2 + 25x2 + 4xy + (−32y2)			Remove the parentheses grouping the polynomial and rewrite any subtraction as addition of the opposite.
		(4x2 +25x2) +[(−12xy)+ 4xy] + [9y2+ (−32y2)]		Group like terms using commutative and associative properties.
		29x2 + (−8xy) +(−23y2)		Combine like terms.
Answer		The sum is 29x2 – 8xy – 23y2.	Rewrite as subtraction.

Some people find that writing the polynomial addition in a vertical form makes it easy to combine like terms. The process of adding the polynomials is the same, but the arrangement of the terms is different. The example below shows this “vertical” method of adding polynomials:

Example
Problem	Add. (3x + 2y – 4z ) + (45x – y + 75z)
	3x + 2y –   4z + 45x –   y + 75z		Write one polynomial below the other, making sure to line up like terms.
	48x + y + 71z		Combine like terms, paying close attention to the signs.
Answer	The sum is 48x + y + 71z.

When there isn't a matching like term for every term in each polynomial, there will be empty places in the vertical arrangement of the polynomials. This layout makes it easy to check that you are combining like terms only.

Example
Problem		Add. (10ab + 15ac – 25bc + 5) + (4ab – 8bc – 12)
		10ab + 15ac – 25bc +   5 +   4ab –   8bc – 12		Write one polynomial below the other, making sure to line up like terms.
	14ab + 15ac – 33bc – 7			Combine like terms, paying close attention to the signs.
Answer		The sum is 14ab + 15ac – 33bc – 7.

Add. (8a3b2 + 6a2b – 4b2 + 5) + (10a2b – 4a3b2 + 6a2 – 7) A) 18a3b2 + 2a2b + 2b2 – 2 B) 4a3b2 + 16a2b + 6a2 – 4b2 – 2 C) 18a3b2 + 2a2b + 6a2 – 4b2 – 2 D) 4a6b4 + 16a4b2 + 6a2 – 4b2 – 2 Show/Hide Answer

Subtracting Polynomials with More Than One Variable

You can apply the same process used to subtract polynomials with one variable to subtract polynomials with more than one variable. In order to remove the parentheses following a subtraction sign, you must multiply each term by −1.

Example
Problem	Subtract. (14x3y2 – 5xy + 14y) – (7x3y2 – 8xy + 10y)
14x3y2 – 5xy + 14y – 7x3y2 + 8xy  – 10y		Remove the parentheses. Notice the signs!
14x3y2  – 7x3y2 – 5xy  + 8xy + 14y – 10y		Regroup to put like terms together. When you regroup or rearrange terms involving subtraction, think of the subtraction as “adding the opposite” and move the negative sign along with the term.
	7x3y2 + 3xy  + 4y	Combine like terms.
Answer	The difference is 7x3y2 + 3xy + 4y.

An alternative to the approach shown above is the vertical method for arranging the subtraction problem. This method is shown below for a different problem. Both methods are effective for subtracting polynomials—the idea is to identify and organize like terms in order to compute with them accurately.

Example
Problem	Subtract. (10a3  + 5b2  – 5c + 10) – (15 + 5c  – 15b2 + 10a3)
	10a3 + 5b2 – 5c + 10   – (10a3 – 15b2 + 5c + 15)	Organize the like terms using the vertical approach.
	0 + 20b2 – 10c – 5	Combine like terms. Pay attention to the signs when subtracting.
Answer	The difference is 20b2 – 10c – 5.

The examples that follow illustrate the left-to-right and vertical methods for the same polynomial subtraction problem. Think about which method you find easier.

Example
Problem		Subtract. (3x4y3 + 5x3y2  –  2x2y2) –  (−2x4y3 + 4x3y2 – 2x2y3 – 1)
3x4y3 + 5x3y2  –  2x2y2 + 2x4y3 – 4x3y2 + 2x2y3 + 1			Remove the parentheses. The first polynomial stays the same. The signs change in the second polynomial.
3x4y3 + 2x4y3 + 5x3y2 – 4x3y2  –  2x2y2 + 2x2y3 + 1			Regroup using commutative and associative properties.
5x4y3 + x3y2 –  2x2y2 + 2x2y3 + 1			Combine like terms.
Answer	The difference is 5x4y3 + x3y2 – 2x2y2 + 2x2y3 + 1.

Example
Problem	Subtract. (3x4y3 + 5x3y2 – 2x2y2) –  (−2x4y3 + 4x3y2 – 2x2y3 – 1)
	3x4y3 + 5x3y2 – 2x2y2 – (−2x4y3 + 4x3y2 – 2x2y3 – 1)	Write one polynomial below the other, making sure to line up like terms.
	5x4y3 +  x3y2 – 2x2y2 + 2x2y3 + 1	Combine like terms, paying close attention to the signs.
Answer	The difference is 5x4y3 + x3y2 – 2x2y2+ 2x2y3 + 1.

Multiplying Polynomials with More Than One Variable

Polynomials with more than one variable can also be multiplied by one another. You use the same techniques you used when you multiplied polynomials with only one variable. Consider the following example.

(4x²y³)(5x⁴y²)

This is an example of multiplication of two polynomials, specifically monomials, with two variables. To do this multiplication, you multiply the coefficients and use the rules of exponents to find the exponent for each variable in order to find the product. Let’s look.

(4x²y³)(5x⁴y²) = (4 • 5)(x²⁺⁴)(y³⁺²) = 20x⁶y⁵

To multiply a monomial by a binomial, you use the distributive property in the same way as multiplying polynomials with one variable.

Example
Problem	Multiply.
		Multiply, using the distributive property.
Answer	The product is.

To multiply two binomials containing more than one variable, you can still use the FOIL (First, Outer, Inner, Last) method that works for binomials with one variable. After all, FOIL is simply a shortcut for using the distributive property to multiply each term in one binomial by each term in the other binomial. This process works for multiplying any two binomials. Two examples follow.

Example
Problem	Multiply. (4x – 7xy)(2y + 3x)
	4x • 2y = 8xy		First
	4x • 3x = 12x2		Outer
	−7xy • 2y = −14xy2		Inner
	−7xy • 3x = −21x2y		Last
			Be careful about including the negative sign with −7xy, since this term is being subtracted.
		8xy + 12x2 – 14xy2 – 21x2y	Combine terms into one expression.
Answer	The product is 8xy + 12x2 – 14xy2 – 21x2y.

The next example shows the product of a binomial and a trinomial, each with two variables. Since FOIL can only be used with the product of two binomials, you need to systematically multiply each term in the binomial by each term in the trinomial.

Example
Problem		Multiply. (9b – ab)(5a2b + 7ab – b)
		9b(5a2b + 7ab – b) 45a2b2 + 63ab2 – 9b2  −ab(5a2b + 7ab – b) −5a3b2 – 7a2b2 + ab2	Multiply 9b by each term in the trinomial, paying attention to the signs. Multiply −ab by each term in the trinomial, paying attention to the signs.
45a2b2 + 63ab2 – 9b2 – 5a3b2 – 7a2b2 + ab2			Combine the products.
45a2b2 + 63ab2 – 9b2 - 5a3b2 – 7a2b2 + ab2 38a2b2 + 64ab2 – 9b2 – 5a3b2			Combine like terms.
Answer	The product is 38a2b2 + 64ab2 – 9b2 – 5a3b2.

When multiplying multivariable polynomials like this, some people prefer to set up the multiplication in a vertical fashion—as you would do if you were multiplying 45 • 189. The example below shows (9b – ab)(5a²b + 7ab – b) set up in vertical fashion.

Example
Problem	(9b – ab)(5a2b + 7ab – b)
	9b −ab x 5a2b + 7ab −b −9b2 + ab2		Set up the problem in a vertical form, and begin by multiplying 9b – ab by −b. Make sure to pay attention to the signs! Place the products underneath, as shown.
		9b −ab x 5a2b + 7ab −b - 9b2 + ab2 −7a2b2 + 63ab2	Now multiply 9b – ab by +7ab. Notice that (9b)(7ab) = 63ab2; since this term is like ab2, place it directly beneath it.
		9b −ab x 5a2b + 7ab −b −9b2 + ab2 −7a2b2 + 63ab2 −5a3b2 + 45a2b2	Finally, multiply 9b – ab by 5a2b.
		9b −ab 5a2b + 7ab −b - 9b2 + ab2 −7a2b2 + 63ab2 - 5a3b2 + 45a2b2 - 5a3b2 + 38a2b2 - 9b2 + 64ab2	Now add like terms.
Answer	−5a3b2 + 38a2b2 – 9b2 + 64ab2

Notice that the products of the two examples are the same, although the order of the individual terms is different due to the different solution methods.

Find the product. −4pt2(5pt3 + 3pt2 – t) A) −20p2t5 – 12p2t4 + 4pt3 B) −20t5 + 12p2t4 – 4pt3 C) −20pt6 – 12pt4 + 4pt2 D) −20p2t5 + 3pt2 – t Show/Hide Answer

Dividing Polynomials with More Than One Variable

The fourth arithmetic operation is division. Polynomials with more than one variable can also be divided. When dividing monomials with more than one variable, you divide the coefficients and then divide variables. When there are exponents with the same base, the law of exponents says you divide by subtracting the exponents. Consider this example.

Example
Problem	Divide.
			To make it easier, you can break up the coefficients and variables into numeric and variable factors.
			Divide the coefficients, and divide the variables by subtracting the exponents with like bases.
			Rewrite with positive exponents.
Answer	The quotient is.

Now let’s look at an example of dividing a trinomial with more than one variable by a monomial with more than one variable. This follows the same procedure as when you have one variable, but you need to pay attention to distinguishing between the variables.

Example
Problem	Divide.
		To make it easier, you can break the division out by the terms in the polynomial since each term is being divided by 2x2y.
		Perform the division of each term by dividing the coefficients and dividing the variables by subtracting the exponents of variables with like bases.
Answer	The quotient is .

Divide. A) 5st2 – 2s2t + 1 B) 5st2 – 10s3t3 + 5st2 C) 20st2 – 5s2t D)  Show/Hide Answer

Summary

Performing addition, subtraction, multiplication, and division of polynomials with more than one variable follows the same steps as operating on polynomials in one variable. The key things to pay attention to are combining only like terms and applying the laws of exponents, integer operations, and the order of operations accurately.

http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U11_L3_T2_text_final.html

Algebra1

The slope of a linear function

The steepness of a hill is called a slope. The same goes for the steepness of a line. The slope is defined as the ratio of the vertical change between two points, the rise, to the horizontal change between the same two points, the run.

slope=riserun=changeinychangeinx$$slope=\frac{rise}{run}=\frac{changeiny}{changeinx}$$

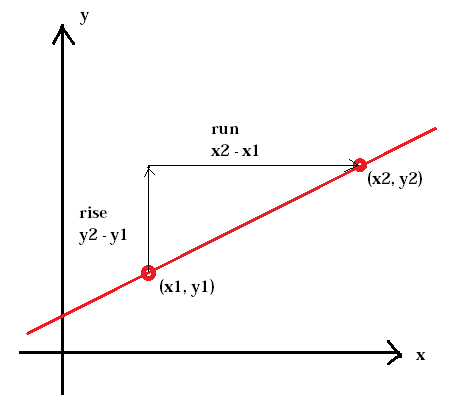
The slope of a line is usually represented by the letter m. (x₁, y₁) represents the first point whereas (x₂, y₂) represents the second point.

m=y2−y1x2−x1$$m=\frac{y_2-y_1}{x_2-x_1}$$

It is important to keep the x-and y-coordinates in the same order in both the numerator and the denominator otherwise you will get the wrong slope.

---

Example

Find the slope of the line

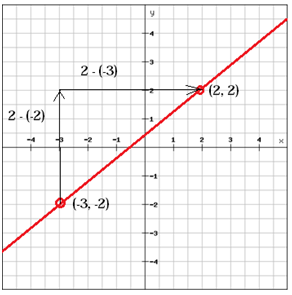
(x₁, y₁) = (-3, -2) and (x₂, y₂) = (2, 2)

m=y2−y1x2−x1=2−(−2)2−(−3)=2+22+3=45$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-\left(-2\right)}{2-\left(-3\right)}=\frac{2+2}{2+3}=\frac{4}{5}$$

A line with a positive slope (m > 0), as the line above, rises from left to right whereas a line with a negative slope (m < 0) falls from left to right.

m=y2−y1x2−x1=(−1)−32−(−2)=−1−32+2=−44=−1$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{\left(-1\right)-3}{2-\left(-2\right)}=\frac{-1-3}{2+2}=\frac{-4}{4}=-1$$

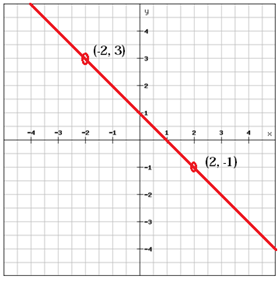
If two lines have the same slope the lines are said to be parallel.

---

You can express a linear function using the slope intercept form.

y=mx+b$$y=mx+b$$

m=slope$$m=slope$$

 b=y−intercept