Logarithms are the "opposite" of exponentials, just as subtraction is the opposite of addition and division is the opposite of multiplication. Logs "undo" exponentials. Technically speaking, logs are the inverses of exponentials.
In practical terms, I have found it useful to think of logs in terms of The Relationship:
| —The Relationship— | |||
|
On the left-hand side above is the exponential statement "y = bx". On the right-hand side above, "logb(y) = x" is the equivalent logarithmic statement, which is pronounced "log-base-b of y equals x"; The value of the subscripted "b" is "the base of the logarithm", just as b is the base in the exponential expression "bx". And, just as the base b in an exponential is always positive and not equal to 1, so also the base bfor a logarithm is always positive and not equal to 1. Whatever is inside the logarithm is called the "argument" of the log. Note that the base in both the exponential equation and the log equation (above) is "b", but that the x and y switch sides when you switch between the two equations.
| —The Relationship Animated— |
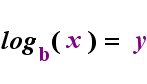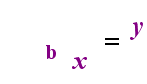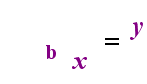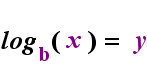 |
If you can remember this relationship (that whatever had been the argument of the log becomes the "equals" and whatever had been the "equals" becomes the exponent in the exponential, and vice versa), then you shouldn't have too much trouble with logarithms.
(I coined the term "The Relationship" myself. You will not find it in your text, and your teachers and tutors will have no idea what you're talking about if you mention it to them. "The Relationship" is entirely non-standard terminology. Why do I use it anyway? Because it works.)
By the way: If you noticed that I switched the variables between the two boxes displaying "The Relationship", you've got a sharp eye. I did that on purpose, to stress that the point is not the variables themselves, but how they move.
- Convert "63 = 216" to the equivalent logarithmic expression.
To convert, the base (that is, the 6)remains the same, but the 3 and the 216 switch sides. This gives me:
log6(216) = 3 Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
- Convert "log4(1024) = 5" to the equivalent exponential expression.
- Simplify log2(8).
- Simplify log5(25).
- Simplify log64(4). Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
- Simplify log6(6).
- Simplify log3(1).
- Simplify log4(–16).
- Simplify log2(0).
- Simplify logb(b3).
- Simplify 2log2(9).
- The Relationship: "logb(x) = y" means the same thing as "b y = x".
- Logarithms are really exponents (powers); they're just written differently.
- logb(b) = 1, for any base b, because b1 = b.
- logb(1) = 0, for any base b, because b0 = 1.
- logb(a) is undefined if a is negative.
- logb(0) is undefined for any base b.
- logb(bn) = n, for any base b.
This log is equal to some number, which I'll call y. This naming gives me the equation log2(8) = y. Then the Relationship says:
2 y = 8
That is, log2(8), also known as y, is the power that, when put on 2, will turn 2 into 8. The power that does this is 3:
23 = 8
Since 2 y = 8 = 23, then it must be true that y = 3, and I get:
log2(8) = 3
The Relationship says that, since log5(25) = y, then 5 y = 25. This means that the given log log5(25) is equal to the power y that, when put on 5, turns 5 into 25. The required power is 2, because 52 = 25. Then 52 = 5 y= 25, so:
log5(25) = 2
The Relationship says that this log represents the power y that, when put on 64, turns it into 4. Remembering that 43 is 64, and remembering that fractional exponents correspond to roots, this means that the cube root of 64 is 4, so 64(1/3) = 4. Then:
log64(4) = 1/3
This last example highlights the fact that, to be able to work intelligently with logs, you need to be pretty good with your exponents. So take the time to review them, if you're feeling a little shaky.
The Relationship says that, since log6(6) = y, then 6 y = 6. But 6 = 61, so 6 y = 61, and y = 1. That is:
log6(6) = 1
This is always true: logb(b) = 1 for any base b, not just for b = 6.
The Relationship says that, since log3(1) = y, then 3 y = 1. But 1 = 30, so 3 y = 30, and y = 0. That is:
log3(1) = 0
This is always true: logb(1) = 0 for any base b, not just for b = 3.
The Relationship says that, since log4(–16) = y, then 4 y = –16. But wait! What power y could possibly turn a positive 4 into a negative 16? This just isn't possible, so the answer is:
no solution
This is always true: logb(a) is undefined for any negative argument a, regardless of what the base is.
The Relationship says that, since log2(0) = y, then 2 y = 0. But wait! What power y could possibly turn a 2 into a zero? This just isn't possible, so the answer is:
no solution
This is always true: logb(0) is undefined for any base b, not just for b = 2.
The Relationship says that "logb(b3) = y" means "b y = b3". Then clearly y = 3, so:
logb(b3) = 3
This is always true: logb(bn) = n for any base b.
Some students like to think of the above simplification as meaning that the b and the log-base-b "cancel out". This is not technically correct, but it can be a useful way of thinking of things. Just don't say it out loud in front of your instructor.
Remember that a logarithm is just a power; it's a lumpy and long way of writing the power, but it's just a power, nonetheless. The expression "log2(9)" means "the power which, when put on 2, turns 2 into 9." And they've put that power onto 2, which means that the 2 has been turned into 9!
Looking at it another way, "2log2(9) = y" means "log2(y) = log2(9)" (which is the equivalent logarithmic statement), so y = 9. But y = 2log2(9), so 2log2(9) = 9.
While the second way is technically correct, I find the first way to be more intuitive and understandable. Either way, though, I get an answer of:
2log2(9) = 9
This last example probably looks very complicated, and, in the technical explanation, it is. Look instead at the intuitive explanation (in the first paragraph). Some students even view the above problem as the 2 and the log-base-2 as "cancelling out", which is not technically correct, but can be a useful way of remembering how this type of problem works.
To synopsize, these are the things you should know from this lesson so far:
- Simplify log(100).
- Simplify log(98).
- Simplify ln(e4.5).
- Simplify ln(2). Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
To convert, the base (that is, the 4) remains the same, but the 1024 and the 5 switch sides. This gives me:
A logarithm can have any positive value as its base, but two log bases are more useful than the others. The base-10, or "common", log is popular for historical reasons, and is usually written as "log(x)". For instance, pH (the measure of a substance's acidity or alkalinity), decibels (the measure of sound intensity), and the Richter scale (the measure of earthquake intensity) all involve base-10 logs. If a log has no base written, you should generally (in algebra classes) assume that the base is 10.
The other important log is the "natural", or base-e, log, denoted as "ln(x)" and usually pronounced as "ell-enn-of-x". (Note: That's "ell-enn", not "one-enn" or "eye-enn"!) Just as the number e arises naturally in math and the sciences, so also does the natural log, which is why you need to be familiar with it.
Warning: If you eventually progress to much-more advanced mathematics, you may find that sometimes "log(x)" means the base-e log or even base-2 log, rather than the common log.
Because the common and natural logs are pretty much the only logs that are used "in real life", these are the only two for which you have calculator keys. Make sure you know where these keys are, and how to use them.
Aside: Why would the "natural log" be denoted by "ln", rather than by "nl"? One popular idea relates to Euler ("OY-lur"), the guy who discovered (invented?) the natural exponential. Euler was Swiss and spoke French, so he might have called the function "le Logarithme Naturel", rather than "the natural log", in which case, "ln" makes sense. However, history shows that Euler actually used just "l(x)" for the logarithm using "his" number e as its base.
The first published use of the "ln" notation for the base-e logarithm was Stringham's, in his 1893 text "Uniplanar Algebra". Prof. Stringham was an American, so I have no idea why he would have used the notation "ln", other than perhaps to reflect a common, though mistaken, idea that Napier's log was a base-e log. That is, "ln" might have meant to stand for "Log of Napier".
It is even possible that the "ln" notation is a mistake: A European mathematician once proposed abbreviating "log" as "lg" and then using a script "l" for the function, with, effectively, a little squiggle afterwards which was meant to indicate a subscripted italic "g". But in the graphic I've seen, the "g" looks much more like an "n". Some of the other proposed notations for the natural logarithm were even more odd.
Mercator (not the map guy) used a Latin form of the term, "log naturalis" in his 1668 book on logarithms, and, as of the late 1800s, various English-speakers were using the notation "log.nat." for the natural logarithm. In short, the origin of this notation seems somewhat obscure, perhaps even unknown, which is unusual for such a recent "invention".
Since 100 = 102, then log(100) = log(102) = 2, because "log(100) = y" means "10 y = 100 = 102", so y = 2.
log(100) = 2
Plug "log(100)" into your calculator, and you'll get the same answer.
Since 98 is not a nice neat power of 10 (the way that 100 was), I cannot be clever with exponents to arrive at an exact answer. On this exercise, I am stuck with using my calculator to get an approximate value. So I'll plug this into my calculator, remembering to use the "LOG" key (not the "LN" key), and I get log(98) = 1.99122607569..., or:
log(98) = 1.99, rounded to two decimal places
Remember that "ln( )" means the base-e log, so "ln(e4.5)" might be thought of as "loge(e4.5)". The Relationship says that "ln(e4.5) = y" means "e y = e4.5", so y = 4.5, and:
ln(e4.5) = 4.5
Plug "ln(e4.5)" into your calculator, and you'll get the same answer. (Make sure you put parentheses around the "e4.5", so the calculator knows that the exponent is inside the log.)
Since 2 is a nice neat whole number and since e isn't, then it is unlikely that 2 is a nice neat power of e. So I can't simplify this expression by being clever with exponents. Instead, I'll have to evaluate this in my calculator, getting an approximate answer of ln(2) = 0.69314718056...,
Source:
https://www.purplemath.com/modules/logs3.htm
No comments:
Post a Comment