Week of February 7, 2020 College Readiness Math

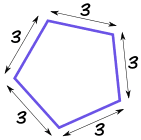
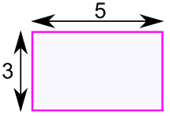
Perimeter

Perimeter is the distance around a two-dimensional shape.

Example: the perimeter of this rectangle is 7+3+7+3 = 20

Example: the perimeter of this regular pentagon is:

3+3+3+3+3 = 5×3 = 15

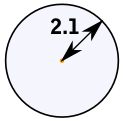
The perimeter of a circle is called the circumference: Circumference = 2π × radius

Perimeter Formulas

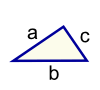		Triangle Perimeter = a + b + c
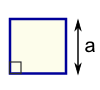		Square Perimeter = 4 × a a = length of side
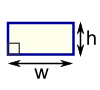		Rectangle Perimeter = 2 × (w + h) w = width h = height
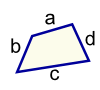		Quadrilateral Perimeter = a + b + c + d
		Circle Circumference = 2πr r = radius
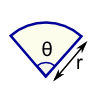		Sector Perimeter = r(θ+2) r = radius θ = angle in radians
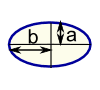		Ellipse Perimeter = very hard! Source: https://www.mathsisfun.com/geometry/perimeter.html

What is Area?

Area is the size of a surface!

Example:

These shapes all have the same area of 9:

It helps to imagine how much paint would cover the shape.

Area of Simple Shapes

There are special formulas for certain shapes:

Example: What is the area of this rectangle?

The formula is:

Area = w × h
w = width
h = height

The width is 5, and the height is 3, so we know w = 5 and h = 3:

Area = 5 × 3 = 15

Learn more at Area of Plane Shapes.

Area by Counting Squares

We can also put the shape on a grid and count the number of squares:

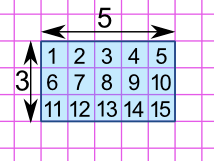
The rectangle has an area of 15

Example: When each square is 1 cm on a side, then the area is 15 cm² (15 square cm)

Approximate Area by Counting Squares

Sometimes the squares don't match the shape exactly, but we can get an "approximate" answer.

One way is:

• more than half a square counts as 1
• less than half a square counts as 0

Like this:

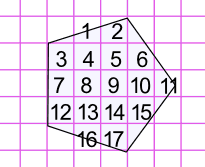
This pentagon has an area of approximately 17

 

Or we can count one square when the areas seem to add up.

Example: Here the area marked "4" seems equal to about 1 whole square (also for "8"):

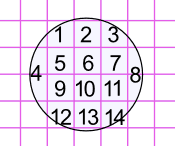
This circle has an area of approximately 14

 

But using a formula (when possible) is best:

Example: The circle has a radius of 2.1 meters:

The formula is:

Area = π × r²

Where:

• π = the number pi (3.1416...)
• r = radius

The radius is 2.1m, so:

Area =3.1416... × (2.1m)²

=3.1416... × (2.1m × 2.1m)

=13.854... m²

So the circle has an area of 13.85 square meters (to 2 decimal places)

Area of Difficult Shapes

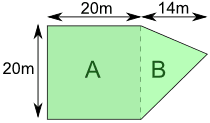
We can sometimes break a shape up into two or more simpler shapes:

Example: What is the area of this Shape?

Let's break the area into two parts:

Part A is a square:

Area of A = a² = 20m × 20m = 400m²

Part B is a triangle. Viewed sideways it has a base of 20m and a height of 14m.

Area of B = ½b × h = ½ × 20m × 14m = 140m²

So the total area is:

Area = Area of A + Area of B

Area = 400m² + 140m²

Area = 540m²

Area by Adding Up Triangles

We can also break up a shape into triangles:

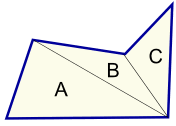
Then measure the base (b) and height (h) of each triangle:

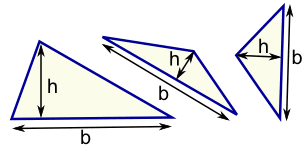
Then calculate each area (using Area = ½b × h) and add them all up.

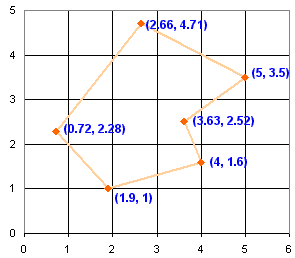
Area by Coordinates

When we know the coordinates of each corner point we can use the Area of Irregular Polygons method.

There is an Area of a Polygon by Drawing Tool that can help too.

 https://www.mathsisfun.com/geometry/area.html