| Solve Inequalities | |
How do you solve a linear inequality and sketch the solution on a number line?
|
How do you solve an absolute value inequality and sketch the solution on a number line?
|
| Investigation | |
| Graphic Organizer | |
| Notes | |
| Practice | |
| Application/Extension | |
| Online Extra Practice |
|
| Textbook Video Tutorials | |
| Regents Prep Text Tutorials | |
| OtherTutorials |
carlisleschools.org
Operations on Complex Numbers
Complex numbers are "binomials" of a sort, and are added, subtracted, and multiplied in a similar way. (Division, which is further down the page, is a bit different.) First, though, you'll probably be asked to demonstrate that you understand the definition of complex numbers.
- Solve 3 – 4i = x + yi Finding the answer to this involves nothing more than knowing that two complex numbers can be equal only if their real and imaginary parts are equal. In other words, 3 = x and –4 = y.
- Simplify (2 + 3i) + (1 – 6i).
- (2 + 3i) + (1 – 6i) = (2 + 1) + (3i – 6i) = 3 + (–3i) = 3 – 3i
- Simplify (5 – 2i) – (–4 – i).
- (5 – 2i) – (–4 – i)
- = (5 – 2i) – 1(–4 – i) = 5 – 2i – 1(–4) – 1(–i)
= 5 – 2i + 4 + i= (5 + 4) + (–2i + i)
= (9) + (–1i) = 9 – i
- Simplify (2 – i)(3 + 4i).
For the last example above, FOILing works for this kind of multiplication, if you learned that method. But whatever method you use, remember that multiplying and adding with complexes works just like multiplying and adding polynomials, except that, while x2 is just x2, i2 is –1. You can use the exact same techniques for simplifying complex-number expressions as you do for polynomial expressions, but you can simplify even further with complexes because i2 reduces to the number –1.
Adding and multiplying complexes isn't too bad. It's when you work with fractions (that is, with division) that things turn ugly. Most of the reason for this ugliness is actually arbitrary. Remember back in elementary school, when you first learned fractions? Your teacher would get her panties in a wad if you used "improper" fractions. For instance, you couldn't say " 3/2 "; you had to convert it to "1 1/2". But now that you're in algebra, nobody cares, and you've probably noticed that "improper" fractions are often more useful than "mixed" numbers. The issue with complex numbers is that your professor will get his boxers in a bunch if you leave imaginaries in the denominator. So how do you handle this?
Suppose you have the following exercise: Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved
Adding and multiplying complexes isn't too bad. It's when you work with fractions (that is, with division) that things turn ugly. Most of the reason for this ugliness is actually arbitrary. Remember back in elementary school, when you first learned fractions? Your teacher would get her panties in a wad if you used "improper" fractions. For instance, you couldn't say " 3/2 "; you had to convert it to "1 1/2". But now that you're in algebra, nobody cares, and you've probably noticed that "improper" fractions are often more useful than "mixed" numbers. The issue with complex numbers is that your professor will get his boxers in a bunch if you leave imaginaries in the denominator. So how do you handle this?
Suppose you have the following exercise: Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved
- Simplify
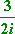
- This is pretty "simple", but they want me to get rid of that i underneath, in the denominator. The 2in the denominator is fine, but the i has got to go. To do this, I will use the fact that i2 = –1. If I multiply the fraction, top and bottom, by i, then the i underneath will vanish in a puff of negativity:
- Simplify
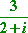
- If I multiply this fraction, top and bottom, by i, I'll get:
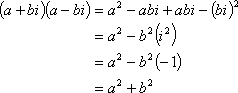
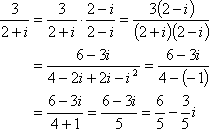
purplemath.com
We can combine polynomials by using the four operations (addition, subtraction, multiplication, and division). This lesson will discuss how we add and subtract polynomials. The next lesson will show you how to multiply polynomials. You will learn how to divide polynomials in Unit 4.
The most important thing to remember when working with polynomials is that they are a group of numbers. This means that each polynomial needs to be in parentheses at the beginning of the problem. However, most of the time there are not a lot of like terms to combine within the parentheses. Therefore, after we combine all of the like terms within the parentheses, we need to get rid of the parentheses.
TASK: How do we get rid of parentheses?
Example: Find the sum of
The key word "sum" indicates that we have to add these two polynomials, so we can set up our problem like this:
Remember to put the parentheses because polynomials are a group!
Since there are no like terms inside each set of parentheses that we can combine, we have to use the distributive property to get rid of the parentheses. However, there's no number outside the parentheses for us to distribute.
TASK: When there's no number outside the parentheses for us to distribute, what number can we put there? Why does this work?
So we get:
When we distributed the positive 1s to both sets of parentheses, we got rid of the parentheses and everything else stayed the same. Then, we combined the like terms to get out answer.
Be careful when combining like terms because the signs of the numbers can get tricky. The easiest way to remember it is that whatever sign is in front of the term is the sign that goes with it. For example, in the problem above, we combine positive 9 and negative 12 to give us the negative 3 in the answer.
Subtracting polynomials is the same as adding polynomials, except there's one step that's a little trickier. Let's look at the same example from above, but instead of adding them, we're going to subtract them. We set up the problem like this:
We still have no numbers outside the parentheses, so we put the ones:
This is where the problem gets a little trickier because this time instead of distributing a positive 1 to each set of parentheses, we're distributing a positive 1 to the first set of parentheses, but a negative 1 to the second set of parentheses. This is going to change the signs of each term in the second polynomial. So we get:
Take a look at one more example. It follows the same steps, but it looks a little different:
TASK: Explain the steps done in the example problem above.