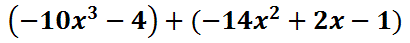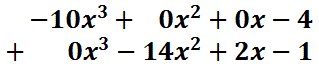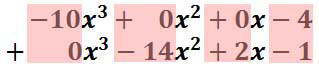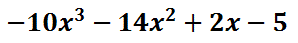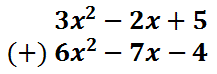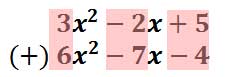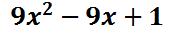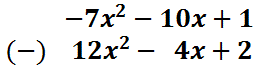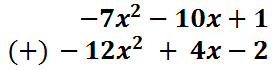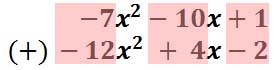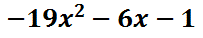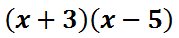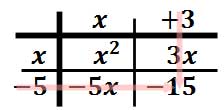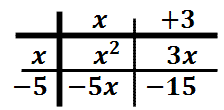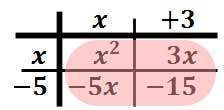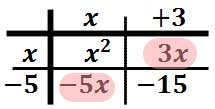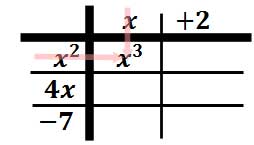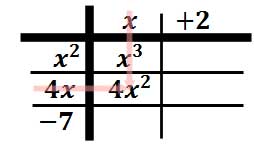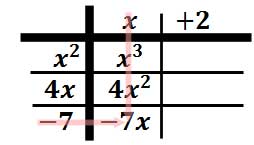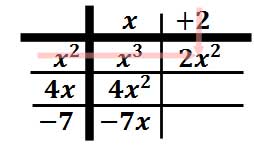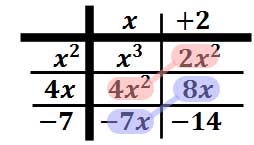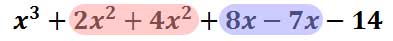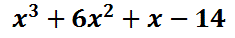Function Notation and Evaluating Function
You've been playing with "y=" sorts of equations for some time now. And you've seen that the "nice" equations (straight lines, say, rather than ellipses) are the ones that you can solve for "y=" and then plug into your graphing calculator. These "y=" equations are functions. But the question you are facing at the moment is "Why do I need this function notation, especially when I've got perfectly nice 'y=', and how does this notation work?"
Think back to when you were in elementary school. Your teacher gave you worksheets containing statements like "[ ] + 2 = 4" and told you to fill in the box. Once you got older, your teacher started giving you worksheets containing statements like "x + 2 = 4" and told you to "solve for x".
Why did your teachers switch from boxes to variables? Well, think about it: How many shapes would you have to use for formulas like the one for the area A of a trapezoid with upper base a, lower base b, and height h? The formula is as follows:
If you try to express the above, or something more complicated, using variously-shaped boxes, you'd quickly run out of shapes. Besides, you know from experience that "A" stands for "area", "h" stands for "height", and "a" and "b" stand for the lengths of the parallel top and bottom sides. Heaven only knows what a square box or a triangular box might stand for!
Why did your teachers switch from boxes to variables? Well, think about it: How many shapes would you have to use for formulas like the one for the area A of a trapezoid with upper base a, lower base b, and height h? The formula is as follows:
If you try to express the above, or something more complicated, using variously-shaped boxes, you'd quickly run out of shapes. Besides, you know from experience that "A" stands for "area", "h" stands for "height", and "a" and "b" stand for the lengths of the parallel top and bottom sides. Heaven only knows what a square box or a triangular box might stand for!
Algebra 2
Assessments: Quiz on Friday, unit test next Thursday, the projected test date.
Monday
Welcome back! Today, we start the class with some applications of polynomials, to ease back into the routine. Then, we move to long division with polynomials, you will do great once you see the pattern. Many of you know I will review the long division from elementary school for the steps.
Help:http://www.purplemath.com/modules/polydiv2.htm
HW; None
Tuesday
We review long division again and look at synthetic division. It is tough at the beginning, yet you will master the process very quickly. We also review factoring today for the rest of the unit needs.
Help:http://www.purplemath.com/modules/synthdiv.htm
HW; None
Wednesday
It is finding roots of polynomials today with synthetic division and factoring. We will review our factoring skills too. I know all of you will love the lesson today.
Help:https://www.khanacademy.org/math/algebra2/arithmetic-with-polynomials/synthetic-division-of-polynomials/v/synthetic-division-example-2
HW; None
Thursday
It is finding roots day three, more advanced with the type of factoring
Help:https://www.khanacademy.org/math/algebra2/arithmetic-with-polynomials/synthetic-division-of-polynomials/v/synthetic-division
HW; Study for quiz tomorrow
Friday
Yes, we made it to Friday! It is quiz day, a day for you to shine. Also, we take notes on 4th degree polynomials.
Help:http://www.mesacc.edu/~scotz47781/mat120/notes/divide_poly/synthetic/synthetic_division.html
HW; None
Have a great weekend!
Monday
Welcome back! Today, we start the class with some applications of polynomials, to ease back into the routine. Then, we move to long division with polynomials, you will do great once you see the pattern. Many of you know I will review the long division from elementary school for the steps.
Help:http://www.purplemath.com/modules/polydiv2.htm
HW; None
Tuesday
We review long division again and look at synthetic division. It is tough at the beginning, yet you will master the process very quickly. We also review factoring today for the rest of the unit needs.
Help:http://www.purplemath.com/modules/synthdiv.htm
HW; None
Wednesday
It is finding roots of polynomials today with synthetic division and factoring. We will review our factoring skills too. I know all of you will love the lesson today.
Help:https://www.khanacademy.org/math/algebra2/arithmetic-with-polynomials/synthetic-division-of-polynomials/v/synthetic-division-example-2
HW; None
Thursday
It is finding roots day three, more advanced with the type of factoring
Help:https://www.khanacademy.org/math/algebra2/arithmetic-with-polynomials/synthetic-division-of-polynomials/v/synthetic-division
HW; Study for quiz tomorrow
Friday
Yes, we made it to Friday! It is quiz day, a day for you to shine. Also, we take notes on 4th degree polynomials.
Help:http://www.mesacc.edu/~scotz47781/mat120/notes/divide_poly/synthetic/synthetic_division.html
HW; None
Have a great weekend!
![[x - 2y = -9] + [-x - 3y = -16] = [-5y = -25]](http://www.purplemath.com/modules/systems/lin016.gif)
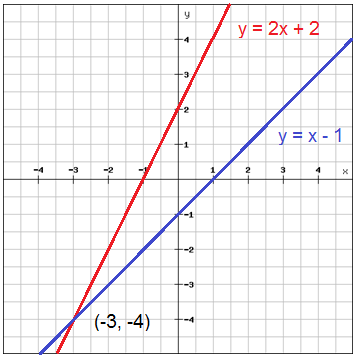
 ideo:
ideo:  uiz:
uiz: