ALGEBRA 1
Exponential Functions: Introduction
Exponential functions look somewhat similar to functions you have seen before, in that they involve exponents, but there is a big difference, in that the variable is now the power, rather than the base. Previously, you have dealt with such functions as f(x) = x2, where the variable x was the base and the number 2 was the power. In the case of exponentials, however, you will be dealing with functions such as g(x) = 2x, where the base is the fixed number, and the power is the variable.
Let's look more closely at the function g(x) = 2x. To evaluate this function, we operate as usual, picking values of x, plugging them in, and simplifying for the answers. But to evaluate 2x, we need to remember how exponents work. In particular, we need to remember that negative exponents mean "put the base on the other side of the fraction line".
So, while positive x-values give us values like these: | | 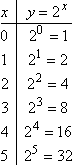
|
...negative x-values give us values like these:
Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved | | 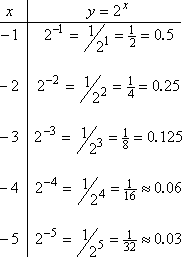
|
Putting together the "reasonable" (nicely graphable) points, this is our T-chart: | | 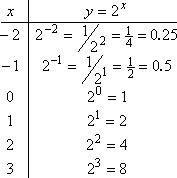
|
...and this is our graph: | | 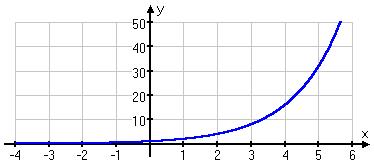
Exponential growth is "bigger" and "faster" than polynomial growth. This means that, no matter what the degree is on a given polynomial, a given exponential function will eventually be bigger than the polynomial. Even though the exponential function may start out really, really small, it will eventually overtake the growth of the polynomial, since it doubles all the time.
For instance, x10 seems much "bigger" than 10x, and initially it is: | | 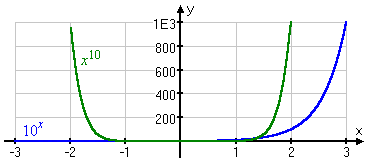
|
But eventually 10x (in blue below) catches up and overtakes x10 (at the red circle below, where x is ten and y is ten billion), and it's "bigger" than x10 forever after: | | 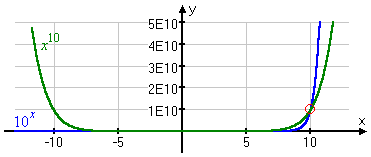
|
Exponential functions always have some positive number other than 1 as the base. If you think about it, having a negative number (such as –2) as the base wouldn't be very useful, since the even powers would give you positive answers (such as "(–2)2 = 4") and the odd powers would give you negative answers (such as "(–2)3 = –8"), and what would you even do with the powers that aren't whole numbers? Also, having 0 or 1 as the base would be kind of dumb, since 0 and 1 to any power are just 0 and 1, respectively; what would be the point? This is why exponentials always have something positive and other than 1 as the base.
Source:http://www.purplemath.com/modules/expofcns.htm
ALGEBRA 2
Monday
Today, we look at the more advanced rational equations, be ready to use FOIL.
Help:http://www.purplemath.com/modules/solverad.htm
HW; None
Tuesday
It is time to look at the combination of rational equations, all types on one page and to review for the test.
Help:https://www.khanacademy.org/math/algebra2/radical-equations-and-functions/solving-square-root-equations/v/solving-radical-equations
HW: ( 1st) Study for test and finish the review sheet
( 3rd) None
Wednesday
1st- test day, be ready
3rd- prepare for test on Thursday
Help:https://www.mathsisfun.com/algebra/radical-equations-solving.html
HW ( 3rd ) study for the test and review sheet
Thursday
3rd - test day! You shall shine!
HW; None
Friday
It is prom tonight and I will not be in class. I will leave practice sheets for you to do or you can work on makeup work.
HW; None
Help: N/A
See you on Monday
Have a great weekend!
|
|
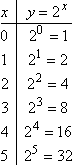
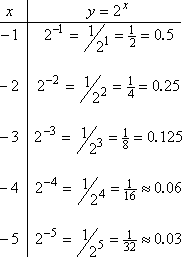
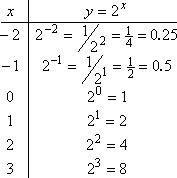



No comments:
Post a Comment