WORD PROBLEMS
WORD PROBLEMS require practice in translating verbal language into algebraic language. See Lesson 1, Problem 8. Yet, word problems fall into distinct types. Below are some examples.
Example 1. ax ± b = c. All problems like the following lead eventually to an equation in that simple form.
Jane spent $42 for shoes. This was $14 less than twice what she spent for a blouse. How much was the blouse?
Solution. Every word problem has an unknown number. In this problem, it is the price of the blouse. Always let x represent the unknown number. That is, let x answer the question.
Let x, then, be how much she spent for the blouse. The problem states that "This" -- that is, $42 -- was $14 less than two times x.
Here is the equation:
| 2x − 14 | = | 42. |
| 2x | = | 42 + 14 (Lesson 9) |
| = | 56. | |
| x | = | 56 2 |
| = | 28. | |
The blouse cost $28.
Example 2. There are b boys in the class. This is three more than four times the number of girls. How many girls are in the class?
Solution. Again, let x represent the unknown number that you are asked to find: Let x be the number of girls.
(Although b is not known, it is not what you are asked to find.)
The problem states that "This" -- b -- is three more than four times x:
| 4x + 3 | = | b. | ||
| Therefore, | ||||
| 4x | = | b − 3 | ||
| x | = | b − 3 4 | . | |
The solution here is not a number, because it will depend on the value of b. This is a type of "literal" equation, which is very common in algebra.
Example 3. The whole is equal to the sum of the parts.
The sum of two numbers is 84, and one of them is 12 more than the other. What are the two numbers?
Solution. In this problem, we are asked to find two numbers. Therefore, we must let x be one of them. Let x, then, be the first number.
We are told that the other number is 12 more, x + 12.
The problem states that their sum is 84:
The line over x + 12 is a grouping symbol called a vinculum. It saves us writing parentheses.
We have:
| 2x | = | 84 − 12 |
| = | 72. | |
| x | = | 72 2 |
| = | 36. | |
This is the first number. Therefore the other number is
x + 12 = 36 + 12 = 48.
The sum of 36 + 48 is 84.
Example 4. The sum of two consecutive numbers is 37. What are they?
Solution. Two consecutive numbers are like 8 and 9, or 51 and 52.
Let x, then, be the first number. Then the number after it is x + 1.
The problem states that their sum is 37:
| 2x | = | 37 − 1 |
| = | 36. | |
| x | = | 36 2 |
| = | 18. | |
The two numbers are 18 and 19.
Example 5. One number is 10 more than another. The sum of twice the smaller plus three times the larger, is 55. What are the two numbers?
Solution. Let x be the smaller number.
Then the larger number is 10 more: x + 10.
The problem states:
| 2x + 3(x + 10) | = | 55. |
| That implies | ||
| 2x + 3x + 30 | = | 55. Lesson 14. |
| 5x | = | 55 − 30 = 25. |
| x | = | 5. |
That's the smaller number. The larger number is 10 more: 15.
Example 6. Divide $80 among three people so that the second will have twice as much as the first, and the third will have $5 less than the second.
Solution. Again, we are asked to find more than one number. We must begin by letting x be how much the first person gets.
Then the second gets twice as much, 2x.
And the third gets $5 less than that, 2x − 5.
Their sum is $80:
| 5x | = | 80 + 5 |
| x | = | 85 5 |
| = | 17. | |
This is how much the first person gets. Therefore the second gets
| 2x | = | 34. |
| And the third gets | ||
| 2x − 5 | = | 29. |
The sum of 17, 34, and 29 is in fact 80.
Algebra 2
Factoring in Algebra
Factors
Numbers have factors:

And expressions (like x2+4x+3) also have factors:

Factoring
Factoring (called "Factorising" in the UK) is the process of finding the factors:
Factoring: Finding what to multiply together to get an expression.
It is like "splitting" an expression into a multiplication of simpler expressions.
Factoring is also the opposite of Expanding:

Common Factor
In the previous example we saw that 2y and 6 had a common factor of 2
But to do the job properly we need the highest common factor, including any variables
More Complicated Factoring
Factoring Can Be Hard !
The examples have been simple so far, but factoring can be very tricky.
Because we have to figure what got multiplied to produce the expression we are given!
It is like trying to find which ingredients
went into a cake to make it so delicious.
It can be hard to figure out!
Experience Helps
With more experience factoring becomes easier.
How can you learn to do that? By getting lots of practice, and knowing "Identities"!
Remember these Identities
Here is a list of common "Identities" (including the "difference of squares" used above).
It is worth remembering these, as they can make factoring easier.
 | ||
| a2 − b2 | = | (a+b)(a−b) |
| a2 + 2ab + b2 | = | (a+b)(a+b) |
| a2 − 2ab + b2 | = | (a−b)(a−b) |
| a3 + b3 | = | (a+b)(a2−ab+b2) |
| a3 − b3 | = | (a−b)(a2+ab+b2) |
| a3+3a2b+3ab2+b3 | = | (a+b)3 |
| a3−3a2b+3ab2−b3 | = | (a−b)3 |
There are many more like those, but those are the most useful ones.
Advice
The factored form is usually best.
When trying to factor, follow these steps:
- "Factor out" any common terms
- See if it fits any of the identities, plus any more you may know
- Keep going till you can't factor any more
There are also Computer Algebra Systems (called "CAS") such as Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce and many more that are good at factoring.
More Examples
Experience does help, so here are more examples to help you on the way:
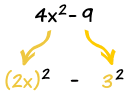
No comments:
Post a Comment